The SSM Procedure

Multivariate ARMA

You can specify a state vector that follows a multivariate autoregressive, moving average (VARMA) model by using the STATE statement option TYPE=VARMA . The autoregressive and moving average orders can be either 0 or 1 ($0 \leq p \leq 1$ and $0 \leq q \leq 1$ )—that is, only VAR(1), MA(1), and VARMA(1,1) models can be specified. The notation and the state space form of the VARMA model described here is taken from Reinsel (1997), which is a good reference for VARMA modeling.

A dim-dimensional vector process $\pmb {\zeta }_{t}$ follows a zero-mean, autoregressive order p, moving average order q (VARMA(p, q)) model if it satisfies the following matrix difference equation:

\[ \pmb {\zeta }_{t} = \sum _{i=1}^{p} \pmb {\Phi }_{i} \pmb {\zeta }_{t-i} + \pmb {\epsilon }_{t} - \sum _{j=1}^{q} \pmb {\Theta }_{j} \pmb {\epsilon }_{t-i} \]

Here $ \pmb {\Phi }_{i}$ and $ \pmb {\Theta }_{j}$ are dim-dimensional square matrices and $ \pmb {\epsilon }_{t}$ is a dim-dimensional, Gaussian, white noise sequence with covariance matrix $\pmb {\Sigma }$. If autoregressive order p is 0, the term that involves $\pmb {\Phi }_{i}$ is absent; similarly, if the moving average order q is 0, the term that involves $ \pmb {\Theta }_{j}$ is absent. Since AR and MA orders can be at most 1, the subscripts of $ \pmb {\Phi }_{i}$ and $ \pmb {\Theta }_{j}$ can be ignored in this discussion—when applicable, an AR coefficient matrix is denoted by $ \pmb {\Phi }$ and an MA coefficient matrix is denoted by $ \pmb {\Theta }$. The unknown elements of $\pmb {\Phi }$, $ \pmb {\Theta }$, and $\pmb {\Sigma }$ constitute the parameter vector that is associated with a VARMA state. The process $\pmb {\zeta }_{t}$ defined by the VARMA difference equation is stationary and invertible (Reinsel, 1997) if and only if the eigenvalues of $\pmb {\Phi }$ and $\pmb {\Theta }$ are strictly less than 1 in magnitude. By default, the SSM procedure imposes these stationarity and invertibility restrictions on $\pmb {\Phi }$ and $\pmb {\Theta }$. However, you can specify $\pmb {\Phi }$ to be an identity matrix, in which case the resulting process is nonstationary.

A VARMA model can be cast into a state space form. The state space form used by the SSM procedure is described in Reinsel (1997, pp 52–53). The system matrices for the supported VARMA models are as follows:

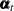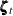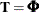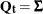  • The VAR(1) form is the simplest. In this case, the underlying state $\pmb {\alpha }_{t}$ is the same as the VAR(1) process $\pmb {\zeta }_{t}$. Therefore, $\mb{T} = \pmb {\Phi }$ and $\mb{Q_ t} = \pmb {\Sigma }$.

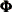  • Taking $\pmb {\Phi }$ equal to the zero matrix if 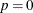$p=0$, the VARMA(1,1) and MA(1) cases can be treated together. In this case, the underlying state 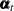$\pmb {\alpha }_{t}$ is 2*dim dimensional and the desired VARMA process 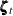$\pmb {\zeta }_{t}$ corresponds to its first dim elements. Let 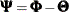$\pmb {\Psi } = \pmb {\Phi } - \pmb {\Theta } $. Then, in the blocked form,

    \[ \mb{T} = \left[ \begin{matrix} \mb{0} & \mb{I}_{dim} \\ \mb{0} & \pmb {\Phi } \\ \end{matrix} \right] \; \; \; \; \text {and} \; \; \; \; \mb{Q}_{t} = \mb{Q} = \left[ \begin{matrix} \pmb {\Sigma } & \pmb {\Sigma } \pmb {\Psi }^{'} \\ \pmb {\Psi } \pmb {\Sigma } & \pmb {\Psi } \pmb {\Sigma } \pmb {\Psi }^{'} \\ \end{matrix} \right] \]

Unless $ \pmb {\Phi }$ is restricted to be identity, the underlying state $\pmb {\alpha }_{t}$ is stationary and the covariance of the initial condition is computed by

\[ \mi{vec}(\mb{Q}_{1}) = (\mb{I} - \mb{T}\bigotimes \mb{T})^{-1} \mi{vec}(\mb{Q}) \]

where $\bigotimes $ denotes the Kronecker product and the $\mi{vec}$ operation on a matrix creates a vector formed by vertically stacking the rows of that matrix. If $ \pmb {\Phi }$ is restricted to be identity, the initial condition is fully diffuse.