The SSM Procedure

Trend Models for Irregular Data

A good reference for these models is De Jong and Mazzi (2001). Throughout this section $h_ t = (\tau _{t+1} - \tau _{t})$ denotes the difference between the successive time points. The system matrices $\mb{T}_{t}$ and $\mb{Q}_{t}$ that govern these models depend on $h_ t$. However, whenever the notation is unambiguous, the subscript t is omitted.

Polynomial Spline Trend

This model is a general-purpose tool for extracting a smooth trend from the noisy data. The order of the spline governs the order of the local polynomial that defines the spline. The order-1 spline corresponds to Brownian motion (continuous-time random walk), the order-2 spline corresponds to integrated Brownian motion (continuous-time integrated random walk), and the order-3 spline provides a locally quadratic trend; the default order is 1. The dimension of the state underlying this component is the same as the order of the spline. The system matrices for the orders up to 3 are described as follows (in all the cases the initial condition is fully diffuse):

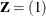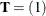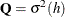
  • order-1 spline: $\mb{Z}= (1)$, $\mb{T}= (1)$, and $\mb{Q}= \sigma ^{2} (h)$

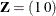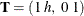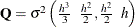
  • order-2 spline: $\mb{Z}= (1\; 0)$, $\mb{T}= (1\; h, \; 0 \; 1)$, and $\mb{Q} = \sigma ^{2} \left( \frac{h^3}{3} \; \; \frac{h^2}{2}, \frac{h^2}{2} \; \; h \right)$

  • order-3 spline: 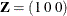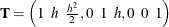$\mb{Z}= (1\; 0\; 0)$, $\mb{T}= \left( 1 \; \; h \; \; \frac{h^2}{2}, 0 \; \; 1 \; \; h, 0 \; \; 0 \; \; 1 \right)$, and

    \[ \mb{Q}[i, j] = \sigma ^{2}* \frac{h^{6-i-j+1}}{(6-i-j+1)(3-i)! (3-j)! } \; \; 1 \leq i, j \leq 3 \]

The system matrices for higher orders are similarly defined (for more information, see De Jong and Mazzi (2001)).

Note that, in addition to providing an estimate of the trend, this methodology can provide estimates of the higher-order derivatives of the trend. If $\pmb {\alpha }$ denotes the k-dimensional subsection that is associated with a polynomial spline of order k, then its $\Mathtext{j}$th element ($1 \leq j \leq k$), $\pmb {\alpha }[j]$, corresponds to the derivative of order $(j-1)$ of this polynomial spline. For an example of the estimation of the first derivative of a trend component, see Example 27.12. For additional information about using these types of trend patterns in data analysis, see Eubank, Huang, and Wang (2003) and Kohn, Ansley, and Tharm (1991).

Decay and Growth Trends

There are two choices for the decay trend: DECAY and DECAY(OU). Similarly, there are two choices for the growth trend: GROWTH and GROWTH(OU). The "OU" stands for the Ornstein-Uhlenbeck form of these models. The decay trend is a sum of two correlated components: one component is a random walk, and the other component is a stationary autoregression. In its Ornstein-Uhlenbeck form, the random walk component is replaced by a constant. The growth trend (and its Ornstein-Uhlenbeck variant) has the same form as the decay trend except that the autoregression is nonstationary (in fact, it is explosive). For growth trend models, floating-point errors can result for even moderately long forecast horizons because of the explosive growth in the trend values.

The system matrices for the decay and the growth types in their respective cases are identical, except for the sign of the rate parameter $\phi $: $\phi < 0.0$ for the decay type, and $\phi > 0.0$ for the growth type. In addition, the initial conditions for the growth models are fully diffuse; they are only partially diffuse for the decay models. The underlying state vector for all these models is two-dimensional.

The system matrices for the DECAY type are:

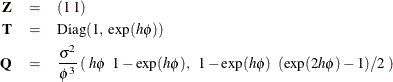
\begin{eqnarray*} \mb{Z} & = & (1 \; 1) \nonumber \\ \mb{T} & = & \mr{Diag} (1, \; \exp (h \phi )) \nonumber \\ \mb{Q} & = & \frac{ \sigma ^{2}}{\phi ^{3}} \left(\; h \phi \; \; 1 - \exp (h \phi ),\; \; 1 - \exp (h \phi )\; \; (\exp (2 h \phi ) - 1)/2 \; \right) \nonumber \end{eqnarray*}

The initial condition is partially diffuse with $\mb{Q_{1}}= \mr{Diag} (0, \; \frac{- \sigma ^{2}}{2 \phi ^{3}} )$. The system matrices for the GROWTH type are the same (with $\phi > 0.0$), except that the initial condition is fully diffuse; so $\mb{Q_{1}}=0$.

For the DECAY(OU) type, $\mb{Z}$ and $\mb{T}$ are the same as DECAY, whereas

\[ \mb{Q}= \mr{Diag} \left(\; 0, \; \sigma ^{2} \frac{(\exp (2 h \phi ) - 1)}{2\phi } \; \right) \; \; \mr{and} \; \; \mb{Q_{1}}= \mr{Diag} (0, \; \frac{- \sigma ^{2}}{2 \phi } ) \]

The system matrices for the GROWTH(OU) type are the same (with $\phi > 0.0$), except that the initial condition is fully diffuse; so $\mb{Q_{1}}=0$.