The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
In addition to being able to specify the system matrices in a flexible way, you can also build a complex model specification
in a modular way by combining simpler subspecifications. Suppose that the state vector for the model to be specified is composed
of subsections that are statistically independent, which is a common scenario in practical modeling situations. For example,
suppose that ![]() can be divided into two disjoint subsections
can be divided into two disjoint subsections ![]() and
and ![]() , which are statistically independent. This entails a corresponding block-diagonal structure to the system matrices
, which are statistically independent. This entails a corresponding block-diagonal structure to the system matrices ![]() ,
, ![]() , and
, and ![]() that govern the state equations. In this case the term
that govern the state equations. In this case the term ![]() that appears in the observation equation also splits into the sum
that appears in the observation equation also splits into the sum ![]() for appropriately partitioned matrices
for appropriately partitioned matrices ![]() and
and ![]() . The model specification syntax of the SSM procedure makes building an SSM from such smaller pieces easy. Throughout this
chapter, the linear combinations of the state subsections (such as
. The model specification syntax of the SSM procedure makes building an SSM from such smaller pieces easy. Throughout this
chapter, the linear combinations of the state subsections (such as ![]() ) that appear in the observation equation are called components. An SSM specification in the SSM procedure is created by combining separate component specifications. In general, you specify
a component in two steps: first you define a state subsection
) that appear in the observation equation are called components. An SSM specification in the SSM procedure is created by combining separate component specifications. In general, you specify
a component in two steps: first you define a state subsection ![]() , and then you define a matching linear combination
, and then you define a matching linear combination ![]() . For some special components, such as some commonly needed trend components, you can combine these two steps into one keyword specification.
. For some special components, such as some commonly needed trend components, you can combine these two steps into one keyword specification.
The following list summarizes the (nonprogramming) SSM procedure syntax statements used for model specification:
-
The ID statement specifies the index variable (
 ). It is assumed that the data within each BY group are ordered (in ascending order) according to the ID variable. The SSM
procedure automatically creates a variable,
). It is assumed that the data within each BY group are ordered (in ascending order) according to the ID variable. The SSM
procedure automatically creates a variable, _ID_DELTA_, which contains the difference between the successive ID values. This variable is available for use by the programming statements to define time-varying system matrices. For example, in the case of SSMs used for modeling the longitudinal data, the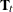 and
and 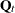 matrices often depend on
matrices often depend on _ID_DELTA_(see Example 27.5). -
The PARMS statement specifies variables that serve as the parameters of the model. That is, it partially defines the model parameter vector
 . Other elements of
. Other elements of  are implicitly defined if your specification of the system matrices is not fully complete.
are implicitly defined if your specification of the system matrices is not fully complete.
-
The STATE statement specifies a subsection of the model state vector. Multiple STATE statements can be used in the model specification; each one defines a statistically independent subsection of the model state vector. For full customization,
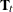 ,
, 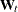 , and
, and 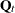 blocks that govern this subsection can be specified as lists of variables that are created by programming statements. However,
you can obtain many commonly needed state subsection types simply by using the TYPE= option in this statement. For example,
the use of TYPE=SEASON(LENGTH=12) results in a state subsection that can be used to define a monthly seasonal component.
blocks that govern this subsection can be specified as lists of variables that are created by programming statements. However,
you can obtain many commonly needed state subsection types simply by using the TYPE= option in this statement. For example,
the use of TYPE=SEASON(LENGTH=12) results in a state subsection that can be used to define a monthly seasonal component.
-
The COMPONENT statement specifies a linear combination that matches a state subsection that is previously defined in a STATE statement. Thus, a matching pair of STATE and COMPONENT statements define a component.
-
The TREND statement is used for easy specification of some commonly needed components that follow stochastic patterns of certain predefined types.
-
The IRREGULAR statement specifies the observation disturbance for a particular response variable.
-
The MODEL statement specifies the observation equation for one of the response variables. A separate MODEL statement is needed for each response variable in the multivariate case. The MODEL statement specifies an equation in which the left-hand side is the response variable and the right-hand side is a list that contains components and regression variables.