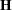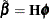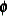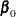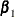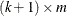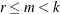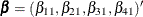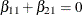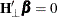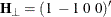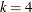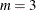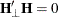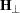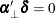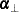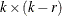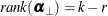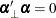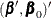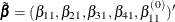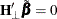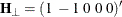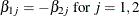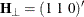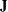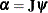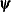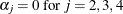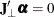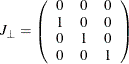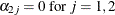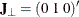The VARMAX Procedure

COINTEG Statement

  • COINTEG RANK=number <options> ;

The COINTEG statement fits the vector error correction model to the data, tests the restrictions of the long-run parameters and the adjustment parameters, and tests for weak exogeneity in the long-run parameters. The P= option in the MODEL statement specifies the autoregressive order of the VECM. Only one COINTEG statement is allowed.

The cointegrated system uses maximum likelihood estimation. If there are no moving average (MA) terms specified by the Q= option in the MODEL statement, no GARCH terms specified in the GARCH statement, and no general restrictions specified in the BOUND and RESTRICT statements, then PROC VARMAX applies the maximum likelihood analysis proposed by Johansen and Juselius (1990); Johansen (1995a, 1995b). Otherwise, the likelihood is maximized using an optimizer whose options can be specified in the NLOPTIONS statement.

The following statements fit a VECM(2): 

proc varmax data=one;
   model y1-y3 / p=2;
   cointeg rank=1;
run;

To test restrictions on $\balpha $ and $\bbeta $, you specify the J= option and the H= option, respectively. You specify the EXOGENEITY option in the COINTEG statement for tests of weak exogeneity in the long-run parameters.

The following example of the COINTEG statement specifies tests of restrictions on $\balpha $ and $\bbeta $, along with tests of weak exogeneity: 

proc varmax data=one;
   model y1-y3 / p=2;
   cointeg rank=1 h=(1 0, -1 0, 0 1)
           j=(1 0, 0 0, 0 1) exogeneity;
run;

You must specify the following option:

RANK=number

specifies the cointegration rank of the cointegrated system. The rank of cointegration should be greater than 0 and less than the number of dependent (endogenous) variables. If number is different from the value of the RANK= option specified in the ECM= option in the MODEL statement, the number specified here is used for the rank.

You can also specify the following options in the COINTEG statement:

ECTREND

specifies the restriction on the drift in the VECM. This option is used in the following cases:

  • There is no separate drift in the VECM, but a constant enters only through the error correction term. For example, for VECM(p),

    \[ \Delta \mb{y} _ t = \balpha (\bbeta ’, \bbeta _0)(\mb{y} _{t-1}’,1)’ + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bepsilon _ t \]

    An example of the ECTREND option follows: 

    model y1 y2 / p=2;
cointeg rank=1 ectrend;

  • There is a separate drift and no separate linear trend in the VECM, but a linear trend enters only through the error correction term. For example, for VECM(p),

    \[ \Delta \mb{y} _ t = \balpha (\bbeta ’, \bbeta _1)(\mb{y} _{t-1}’,t)’ + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bdelta _0 + \bepsilon _ t \]

    An example of the ECTREND option with the TREND= option follows: 

    model y1 y2 / p=2 trend=linear;
cointeg rank=1 ectrend;

If you specify both this option and the NSEASON option in the MODEL statement, then the NSEASON option is ignored. If you specify the NOINT option in the MODEL statement, then this option is ignored.

EXOGENEITY

formulates the likelihood ratio tests for testing weak exogeneity in the long-run parameters. The null hypothesis is that one variable is weakly exogenous for the others.

H=(matrix)

specifies the restrictions $\bH $ on the $k\times r$ or $(k+1)\times r$ cointegrated coefficient matrix $\tilde{\bbeta }$ such that $\tilde{\bbeta } = \bH \bphi $, where $\bH $ is known and $\bphi $ is unknown. If you do not specify the ECTREND option, then the cointegrated coefficient matrix $\tilde{\bbeta }$ is the cointegrating matrix $\bbeta $ and the $\bH $ matrix has dimension $k\times m$. If you specify the ECTREND option, then the cointegrated coefficient matrix $\tilde{\bbeta }$ is the cointegrating matrix $\bbeta $ stacked with the coefficient row vector $\bbeta _0$ or $\bbeta _1$ for the constant or linear trend in the error correction term, and the $\bH $ matrix has dimension $(k+1)\times m$. Here k is the number of dependent variables and m is $r\leq m <k$, where r is defined in the RANK=r option.

For example, consider a VECM(2) with rank equal to 1 on four dependent variables. Then, $\bbeta = (\beta _{11}, \beta _{21}, \beta _{31}, \beta _{41})’$. To test the null hypothesis $\beta _{11} + \beta _{21} = 0$ (that is, $\bH ’_{\bot }\bbeta =0$, where $\bH _\bot = (1\ -1\ 0\ 0)’$), you can use the following statements to specify the restriction matrix $\bH $: 

model y1-y4 / p=2;
cointeg rank=1 h=(1 0 0, -1 0 0, 0 1 0, 0 0 1);

Here the dimension of matrix $\bH $ is $4\times 3$ because $k=4$ and $m=3$, and each row of the matrix $\bH $ is separated by commas. Note that $\bH ’_{\bot }\bH =0$; that is, the $\bH $ and $\bH _{\bot }$ matrices are orthogonal.

When the series has no separate deterministic trend, and therefore you specify the ECTREND option, the constant term should be restricted by $\balpha ’_{\bot }\bdelta = 0$. The matrix $\balpha _{\bot }$ is a $k\times (k-r)$ full-rank matrix orthogonal to $\balpha $, such that $rank(\balpha _{\bot })=k-r$ and $\balpha ’_{\bot }\balpha = 0$. The $\tilde{\bbeta }$ becomes $(\bbeta ’,\bbeta _0)’$ or $\tilde{\bbeta } = (\beta _{11}, \beta _{21}, \beta _{31}, \beta _{41}, \beta _{11}^{(0)})’$. As for the previous test of $\beta _{11} + \beta _{21} = 0$ (that is, $\bH ’_{\bot }\tilde{\bbeta }=0$, where $\bH _\bot = (1\ -1\ 0\ 0\ 0)’$), you can specify the restriction matrix $\bH $ as follows: 

model y1-y4 / p=2;
cointeg rank=1 ectrend
   h=(1 0 0 0, -1 0 0 0, 0 1 0 0, 0 0 1 0, 0 0 0 1);

Because the dimension is changed in the $\bH _{\bot }$ matrix, the dimension of $\bH $ matrix has to be adjusted accordingly.

When the cointegrated system contains three dependent variables and the RANK=2 option is specified, the test of $\beta _{1j}=-\beta _{2j} \; \mbox{for}\; j=1, 2$ can be run with the following restriction matrix $\bH $, where $\bH _\bot = (1\ 1\ 0)’$ and $\bH ’_{\bot }\bbeta =0$: 

cointeg rank=2 h=(1 0, -1 0, 0 1);

There are many ways to achieve a matrix that is orthogonal to a particular matrix. The following statements illustrate how to obtain the orthogonal matrix through QR decomposition: 

proc iml;
   /* For a given matrix H_dot, */
   H_dot = {1 1 0}`;
   /* get its QR decomposition, i.e., H_dot = QR. */
   call qr(Q, R, piv, lindep, H_dot);
   /* Then, the matrix orthogonal to H_dot
      can be extracted from Q. */
   H = Q[,ncol(H_dot)+1:nrow(H_dot)];
   /* Finally, normalize each column of H if necessary. */
   do i = 1 to ncol(H);
      k = 0;
      do j = nrow(H) to 1 by -1;
         if (H[j,i]^=0) then k=j;
      end;
      if (k=0) then
         print "Error: H is not full rank!";
      else
         do j = nrow(H) to 1 by -1;
            H[j,i] = H[j,i] / H[k,i];
         end;
   end;
   print "The given matrix is:";
   print H_dot;
   print "The matrix orthogonal to it is:";
   print H;
quit;
J=(matrix)

specifies the restrictions $\bJ $ on the $k\times r$ adjustment matrix $\balpha $ such that $\balpha =\bJ \bpsi $, where $\bJ $ is known and $\bpsi $ is unknown. The $k\times m$ matrix $\bJ $ is specified by using this option, where k is the number of dependent variables, m is $r\leq m <k$, and r is defined in the RANK=r option.

For example, suppose the system contains four variables, the RANK=1 option is specified, and you want to test $\alpha _ j=0\; \mbox{for}\; j=2, 3, 4$ —that is, $\bJ ’_{\bot }\balpha =0$, where

\begin{eqnarray*} J_{\bot }= \left( \begin{array}{rrr} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \end{eqnarray*}

Then you can specify the restriction matrix $\bJ $ as follows: 

cointeg rank=1 j=(1, 0, 0, 0);

Suppose the system contains three variables, the RANK=2 option is specified, and you want to test $\alpha _{2j}=0\; \mbox{for}\; j=1, 2$—that is, $\bJ ’_{\bot }\balpha =0$, where $\bJ _{\bot } = (0\ 1\ 0)’$. Then you can specify the restriction matrix $\bJ $ as follows: 

cointeg rank=2 j=(1 0, 0 0, 0 1);
NLC

specifies the nonlinear constraints that $\balpha $ and $\bbeta $ are full column rank. Although the constraints are required for a well-defined VECM, only the TECH=QUANEW and TECH=NMSIMP optimization methods in the NLOPTIONS statement support nonlinear constraints. The full-rank constraints are not imposed by default so that other optimization methods, such as TECH=CONGRA or TECH=TRUREG, can be tried. The NLC option works only when numerical optimization is used for estimating VECM (for example, when the BOUND, INITIAL, or RESTRICT statement is specified, or the VEC-ARMA or VEC-ARMA-GARCH model is estimated). That is, the NLC option is ignored if the closed-form solution of parameter estimates and maximum likelihood analysis, which is provided in Johansen and Juselius (1990) and Johansen (1995a, 1995b), can be applied.

NORMALIZE=variable

specifies a single dependent (endogenous) variable whose cointegrating vectors are normalized. If the variable is different from the variable specified in the COINTTEST=(JOHANSEN=) or ECM= option in the MODEL statement, the variable in this option is used. If this option is not specified, cointegrating vectors are not normalized.

If the EXOGENEITY, H=, J=, or NORMALIZE= option is specified, the BOUND, GARCH, INITIAL, and RESTRICT statements are all ignored, and the Q= option in the MODEL statement is also ignored.