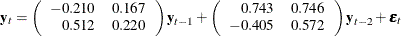The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Vector Error Correction Model
A vector error correction model (VECM) can lead to a better understanding of the nature of any nonstationarity among the different component series and can also improve longer-term forecasting compared to an unconstrained model.
The VECM(p) form with the cointegration rank, 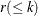 , is written as
, is written as
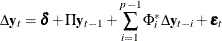
where 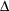 is the differencing operator, such that
is the differencing operator, such that 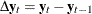 ;
; 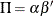 , where
, where  and
and 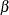 are
are 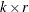 matrices; and
matrices; and 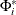 is a
is a 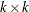 matrix.
matrix.
The VECM(p) form has an equivalent VAR(p) representation as described in the section Vector Autoregressive Model.
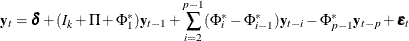
where 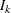 is a
is a 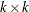 identity matrix.
identity matrix.
An example of the second-order nonstationary vector autoregressive model is
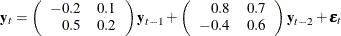
with
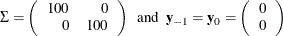
This process can be given the following VECM(2) representation with the cointegration rank one:
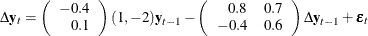
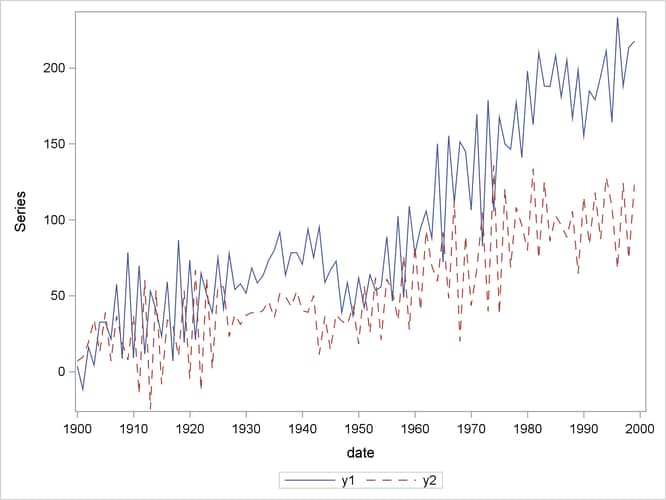
The following PROC IML statements generate simulated data for this VECM(2) form and the PROC SGPLOT statements plot the data, as shown in Figure 42.12:
proc iml;
sig = 100*i(2);
phi = {-0.2 0.1, 0.5 0.2, 0.8 0.7, -0.4 0.6};
call varmasim(y,phi) sigma=sig n=100 initial=0
seed=45876;
cn = {'y1' 'y2'};
create simul2 from y[colname=cn];
append from y;
quit;
data simul2;
set simul2;
date = intnx( 'year', '01jan1900'd, _n_-1 );
format date year4. ;
run;
proc sgplot data=simul2; series x=date y=y1 / lineattrs=(pattern=solid); series x=date y=y2 / lineattrs=(pattern=dash); yaxis label="Series"; run;
Figure 42.12: Plot of Generated Data Process
Cointegration Testing
The following statements use the Johansen cointegration rank test. The COINTTEST=(JOHANSEN) option performs the Johansen trace test and is equivalent to specifying the COINTTEST option with no additional suboptions or specifying the COINTTEST=(JOHANSEN=(TYPE=TRACE)) option.
/*--- Cointegration Test ---*/ proc varmax data=simul2; model y1 y2 / p=2 noint dftest cointtest=(johansen); run;
Figure 42.13 shows the output for Dickey-Fuller tests for the nonstationarity of each series and the Johansen cointegration rank test between series.
Figure 42.13: Dickey-Fuller Tests and Cointegration Rank Test
| Unit Root Test | |||||
|---|---|---|---|---|---|
| Variable | Type | Rho | Pr < Rho | Tau | Pr < Tau |
| y1 | Zero Mean | 1.47 | 0.9628 | 1.65 | 0.9755 |
| Single Mean | -0.80 | 0.9016 | -0.47 | 0.8916 | |
| Trend | -10.88 | 0.3573 | -2.20 | 0.4815 | |
| y2 | Zero Mean | -0.05 | 0.6692 | -0.03 | 0.6707 |
| Single Mean | -6.03 | 0.3358 | -1.72 | 0.4204 | |
| Trend | -50.49 | 0.0003 | -4.92 | 0.0006 | |
| Cointegration Rank Test Using Trace | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | Pr > Trace | Drift in ECM | Drift in Process |
| 0 | 0 | 0.5086 | 70.7279 | <.0001 | NOINT | Constant |
| 1 | 1 | 0.0111 | 1.0921 | 0.3441 | ||
In Dickey-Fuller tests, the second column specifies three types of models, which are zero mean, single mean, or trend. The third column (Rho) and the fifth column (Tau) are the test statistics that are used to test the null hypothesis that the series has a unit root. Other columns are their p-values. You can see that both series have unit roots. For a description of Dickey-Fuller tests, see the section PROBDF Function for Dickey-Fuller Tests in Chapter 6: SAS Macros and Functions.
In the "Cointegration Rank Test Using Trace" table, the last two columns explain the drift in the model or process. Because the NOINT option is specified, the model is
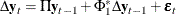
The column Drift in ECM indicates that there is no separate drift in the error correction model, and the column Drift in Process indicates that the process has a constant drift before differencing.
H0 is the null hypothesis, and H1 is the alternative hypothesis. The first row tests the cointegration rank 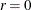 against
against 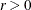 , and the second row tests
, and the second row tests 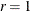 against
against 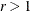 . The trace test statistics in the fourth column are computed by
. The trace test statistics in the fourth column are computed by 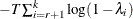 , where T is the available number of observations and
, where T is the available number of observations and 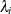 is the eigenvalue in the third column. The p-values for these statistics are output in the fifth column. If you compare the p-value in each row to the significance level of interest (such as 5%), the null hypothesis that there is no cointegrated process
(H0:
is the eigenvalue in the third column. The p-values for these statistics are output in the fifth column. If you compare the p-value in each row to the significance level of interest (such as 5%), the null hypothesis that there is no cointegrated process
(H0: 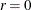 ) is rejected, whereas the null hypothesis that there is at most one cointegrated process (H0:
) is rejected, whereas the null hypothesis that there is at most one cointegrated process (H0: 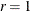 ) cannot be rejected.
) cannot be rejected.
The following statements fit a VECM(2) form to the simulated data:
/*--- Vector Error Correction Model ---*/
proc varmax data=simul2;
model y1 y2 / p=2 noint lagmax=3
print=(iarr estimates);
cointeg rank=1 normalize=y1;
run;
The results in Figure 42.13 indicate that the time series are cointegrated with rank = 1. So you might want to specify the RANK=1 option in the COINTEG
statement. For normalizing the value of the cointegrated vector, you specify the normalized variable by using the NORMALIZE=
option in the COINTEG statement. The COINTEG statement produces the estimates of the long-run parameter,  , and the adjustment coefficient,
, and the adjustment coefficient,  . The PRINT=(IARR) option provides the VAR(2) representation.
. The PRINT=(IARR) option provides the VAR(2) representation.
The VARMAX procedure output is shown in Figure 42.14 through Figure 42.17. In Figure 42.14, "1" indicates the first column of the  and
and  matrices. Because the cointegration rank is 1 in the bivariate system,
matrices. Because the cointegration rank is 1 in the bivariate system,  and
and  are two-dimensional vectors. The estimated cointegrating vector is
are two-dimensional vectors. The estimated cointegrating vector is 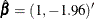 . Therefore, the long-run relationship between
. Therefore, the long-run relationship between 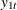 and
and 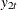 is
is 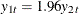 . The first element of
. The first element of 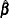 is 1 because
is 1 because 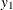 is specified as the normalized variable. Asymptotically,
is specified as the normalized variable. Asymptotically,  follows a normal distribution, and the t values and p-values of its elements are shown in the "Alpha and Beta Parameter Estimates" table; however, because
follows a normal distribution, and the t values and p-values of its elements are shown in the "Alpha and Beta Parameter Estimates" table; however, because  follows a nonnormal distribution, the corresponding standard errors, t values, and p-values are missing. The Variable column shows the variables that correspond to the coefficients. For example, for the coefficient
follows a nonnormal distribution, the corresponding standard errors, t values, and p-values are missing. The Variable column shows the variables that correspond to the coefficients. For example, for the coefficient
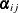 (the ith element in the jth column of
(the ith element in the jth column of  ), ALPHA
), ALPHA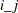 , the variable is the inner product of the transpose of the jth column of
, the variable is the inner product of the transpose of the jth column of  (Beta[,j]
(Beta[,j] ) and the vector of lag 1 dependent variables
) and the vector of lag 1 dependent variables 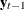 (
( DEP
DEP (t–1)).
(t–1)).
Figure 42.14: Parameter Estimates for the VECM(2) Form
| Type of Model | VECM(2) |
|---|---|
| Estimation Method | Maximum Likelihood Estimation |
| Cointegrated Rank | 1 |
| Beta | |
|---|---|
| Variable | 1 |
| y1 | 1.00000 |
| y2 | -1.95575 |
| Alpha | |
|---|---|
| Variable | 1 |
| y1 | -0.46680 |
| y2 | 0.10667 |
| Alpha and Beta Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | ALPHA1_1 | -0.46680 | 0.04786 | -9.75 | <.0001 | Beta[,1]'*_DEP_(t-1) |
| BETA1_1 | 1.00000 | y1(t-1) | ||||
| D_y2 | ALPHA2_1 | 0.10667 | 0.05146 | 2.07 | 0.0409 | Beta[,1]'*_DEP_(t-1) |
| BETA2_1 | -1.95575 | y2(t-1) | ||||
Figure 42.15 shows the parameter estimates in terms of lag 1 coefficients, 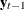 , and lag 1 first-differenced coefficients,
, and lag 1 first-differenced coefficients, 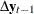 , and their significance. "Alpha * Beta
, and their significance. "Alpha * Beta " indicates the coefficients of
" indicates the coefficients of 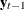 and is obtained by multiplying the Alpha and Beta estimates in Figure 42.14. The parameter AR1
and is obtained by multiplying the Alpha and Beta estimates in Figure 42.14. The parameter AR1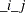 (which is shown in the "Model Parameter Estimates" table) corresponds to the elements in the "Alpha * Beta
(which is shown in the "Model Parameter Estimates" table) corresponds to the elements in the "Alpha * Beta " matrix. The parameter AR2
" matrix. The parameter AR2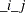 corresponds to the elements in the differenced lagged AR coefficient matrix. The "D_" prefixed to a variable name in Figure 42.15 implies differencing.
corresponds to the elements in the differenced lagged AR coefficient matrix. The "D_" prefixed to a variable name in Figure 42.15 implies differencing.
Figure 42.15: Parameter Estimates for the VECM(2) Form, Continued
| Parameter Alpha * Beta' Estimates | ||
|---|---|---|
| Variable | y1 | y2 |
| y1 | -0.46680 | 0.91295 |
| y2 | 0.10667 | -0.20862 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.74332 | -0.74621 |
| y2 | 0.40493 | -0.57157 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | AR1_1_1 | -0.46680 | 0.04786 | -9.75 | <.0001 | y1(t-1) |
| AR1_1_2 | 0.91295 | 0.09359 | 9.75 | <.0001 | y2(t-1) | |
| AR2_1_1 | -0.74332 | 0.04526 | -16.42 | <.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.74621 | 0.04769 | -15.65 | <.0001 | D_y2(t-1) | |
| D_y2 | AR1_2_1 | 0.10667 | 0.05146 | 2.07 | 0.0409 | y1(t-1) |
| AR1_2_2 | -0.20862 | 0.10064 | -2.07 | 0.0409 | y2(t-1) | |
| AR2_2_1 | 0.40493 | 0.04867 | 8.32 | <.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.57157 | 0.05128 | -11.15 | <.0001 | D_y2(t-1) | |
Figure 42.16 shows the parameter estimates of the innovations covariance matrix and their significance.
Figure 42.16: Parameter Estimates for the VECM(2) Form, Continued
The fitted model is represented as
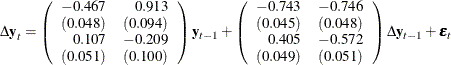
Figure 42.17: Change the VECM(2) Form to the VAR(2) Model
The PRINT=(IARR) option in the previous SAS statements prints the reparameterized coefficient estimates. Because LAGMAX=3 in those statements, the coefficient matrix of lag 3 is zero.
The VECM(2) form in Figure 42.17 can be rewritten as the following second-order vector autoregressive model: