The VARMAX Procedure

Vector Error Correction Model in ARMA Form

The vector error correction model in ARMA form (the VEC-ARMA model) introduces MA terms and is defined as follows:

$\Delta \mb{y} _ t = \balpha \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bepsilon _ t - \sum _{i=1}^{q} \Theta _ i \bepsilon _{t-i}$

The determined terms and the exogenous variables can also be introduced into the model. Similar to the VECM that has only AR terms, the constant term is constrained in the error correction term in Case 2 and the linear trend term is similarly constrained in Case 4.

The model is estimated through the maximum likelihood method. The log likelihood of the model is defined as

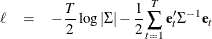
$\begin{eqnarray*} \ell & =& -\frac{T}{2} \log |\Sigma | -\frac{1}{2}\sum _{t=1}^ T \mb{e}_{t}’\Sigma ^{-1}\mb{e}_{t} \end{eqnarray*}$

where

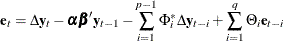
$\begin{eqnarray*} \mb{e}_{t} = \Delta \mb{y} _ t - \balpha \bbeta ’\mb{y} _{t-1} - \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \sum _{i=1}^{q} \Theta _ i \mb{e}_{t-i} \end{eqnarray*}$

conditional on the presample 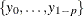$\{ y_0,\ldots ,y_{1-p}\}$ , and $e_ s=0, s \leq 0$ .

You can specify a VEC-ARMA(2,1) model with cointegration rank 2 on the three-dimensional time series by the following statements:

model y1-y3 / p=2 q=1;
cointeg rank=2;

For more information about modeling the cointegrated VARMA processes, see Lütkepohl (2007, Chapter 14).