The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Vector Error Correction Modeling
This section discusses the implication of cointegration for the autoregressive representation.
Consider the vector autoregressive process that has Gaussian errors defined by

or

where the initial values,  , are fixed and
, are fixed and  . The AR operator
. The AR operator 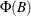 can be re-expressed as
can be re-expressed as
![\[ \Phi (B) = \Phi ^*(B)(1-B)+\Phi (1)B \]](images/etsug_varmax0777.png)
where
![\[ \Phi (1)= I_ k-\Phi _{1}-\Phi _{2}-\cdots -\Phi _{p}, \Phi ^*(B)=I_ k-\sum _{i=1}^{p-1}\Phi ^*_ iB^ i, \Phi ^*_ i= - \sum _{j=i+1}^ p \Phi _ j \]](images/etsug_varmax0778.png)
The vector error correction model (VECM), also called the vector equilibrium correction model, is defined as
![\[ \Phi ^*(B)(1-B)\mb{y} _ t=\balpha \bbeta ’\mb{y} _{t-1} +\bepsilon _ t \]](images/etsug_varmax0779.png)
or
![\[ \Delta \mb{y} _ t = \balpha \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bepsilon _ t \]](images/etsug_varmax0780.png)
where  .
.
- Granger Representation Theorem
-
Engle and Granger (1987) define
![\[ \Pi (z) \equiv (1-z)I_ k - \balpha \bbeta ’ z - \sum _{i=1}^{p-1}{\Phi ^*_ i (1-z)z^ i} \]](images/etsug_varmax0782.png)
and the following assumptions hold:
-
 or
or  .
.
-
The number of unit roots,
 , is exactly
, is exactly 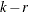 .
.
-
 and
and 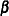 are
are  matrices, and their ranks are both r.
matrices, and their ranks are both r.
Then
 has the representation
has the representation
![\[ y_ t = C \sum _{i=1}^{t}{\bepsilon _ i} + C^*(B)\bepsilon _ t + y_0^* \]](images/etsug_varmax0786.png)
where the Granger representation coefficient, C, is
![\[ C = \bbeta _{\bot } \left[ \balpha ’_{\bot } \Phi (1) \bbeta _{\bot } \right]^{-1} \balpha ’_{\bot } \]](images/etsug_varmax0787.png)
where the full-rank
 matrix
matrix 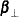 is orthogonal to
is orthogonal to 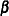 and the full-rank
and the full-rank  matrix
matrix 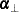 is orthogonal to
is orthogonal to  .
.  is an
is an  process, and
process, and  depends on the initial values.
depends on the initial values.
-
The Granger representation coefficient C can be defined only when the  matrix
matrix  is invertible.
is invertible.
One motivation for the VECM(p) form is to consider the relation  as defining the underlying economic relations. Assume that agents react to the disequilibrium error
as defining the underlying economic relations. Assume that agents react to the disequilibrium error  through the adjustment coefficient
through the adjustment coefficient  to restore equilibrium. The cointegrating vector,
to restore equilibrium. The cointegrating vector, 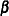 , is sometimes called the long-run parameter.
, is sometimes called the long-run parameter.
Consider a vector error correction model that has a deterministic term, 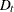 , which can contain a constant, a linear trend, and seasonal dummy variables. Exogenous variables can also be included in
the model. The model has the form
, which can contain a constant, a linear trend, and seasonal dummy variables. Exogenous variables can also be included in
the model. The model has the form

where  .
.
The alternative vector error correction representation considers the error correction term at lag  and is written as
and is written as
![\[ \Delta \mb{y} _ t=\sum _{i=1}^{p-1}\Phi ^{\sharp }_ i\Delta \mb{y} _{t-i} +\Pi ^{\sharp } \mb{y} _{t-p} + A D_ t +\sum _{i=0}^{s}\Theta ^*_ i\mb{x} _{t-i} +\bepsilon _ t \]](images/etsug_varmax0797.png)
If the matrix  has a full rank (
has a full rank ( ), all components of
), all components of 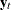 are
are  . On the other hand,
. On the other hand, 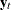 are stationary in difference if
are stationary in difference if  . When the rank of the matrix
. When the rank of the matrix  is
is  , there are
, there are 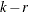 linear combinations that are nonstationary and r stationary cointegrating relations. Note that the linearly independent vector
linear combinations that are nonstationary and r stationary cointegrating relations. Note that the linearly independent vector  is stationary and this transformation is not unique unless
is stationary and this transformation is not unique unless 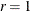 . There does not exist a unique cointegrating matrix
. There does not exist a unique cointegrating matrix 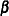 because the coefficient matrix
because the coefficient matrix  can also be decomposed as
can also be decomposed as

where M is an  nonsingular matrix.
nonsingular matrix.
Test for Cointegration
The cointegration rank test determines the linearly independent columns of  . Johansen and Juselius proposed the cointegration rank test by using the reduced rank regression (Johansen 1988, 1995b; Johansen and Juselius 1990).
. Johansen and Juselius proposed the cointegration rank test by using the reduced rank regression (Johansen 1988, 1995b; Johansen and Juselius 1990).
Different Specifications of Deterministic Trends
When you construct the VECM(p) form from the VAR(p) model, the deterministic terms in the VECM(p) form can differ from those in the VAR(p) model. When there are deterministic cointegrated relationships among variables, deterministic terms in the VAR(p) model are not present in the VECM(p) form. On the other hand, if there are stochastic cointegrated relationships in the VAR(p) model, deterministic terms appear in the VECM(p) form via the error correction term or as an independent term in the VECM(p) form. There are five different specifications of deterministic trends in the VECM(p) form.
-
Case 1: There is no separate drift in the VECM(p) form.
![\[ \Delta \mb{y} _ t = \balpha \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} +\bepsilon _ t \]](images/etsug_varmax0803.png)
-
Case 2: There is no separate drift in the VECM(p) form, but a constant enters only via the error correction term.
![\[ \Delta \mb{y} _ t = \balpha (\bbeta ’, \bbeta _0)(\mb{y} _{t-1}’,1)’ + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bepsilon _ t \]](images/etsug_varmax0120.png)
-
Case 3: There is a separate drift and no separate linear trend in the VECM(p) form.
![\[ \Delta \mb{y} _ t = \balpha \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bdelta _0 + \bepsilon _ t \]](images/etsug_varmax0804.png)
-
Case 4: There is a separate drift and no separate linear trend in the VECM(p) form, but a linear trend enters only via the error correction term.
![\[ \Delta \mb{y} _ t = \balpha (\bbeta ’, \bbeta _1)(\mb{y} _{t-1}’,t)’ + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bdelta _0 + \bepsilon _ t \]](images/etsug_varmax0121.png)
-
Case 5: There is a separate linear trend in the VECM(p) form.
![\[ \Delta \mb{y} _ t = \balpha \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + \bdelta _0 + \bdelta _1t + \bepsilon _ t \]](images/etsug_varmax0805.png)
First, focus on Cases 1, 3, and 5 to test the null hypothesis that there are at most r cointegrating vectors. Let
![\begin{eqnarray*} Z_{0t}& =& \Delta \mb{y} _ t \\ Z_{1t}& =& \mb{y} _{t-1} \\ Z_{2t}& =& [\Delta \mb{y} _{t-1}’,\ldots ,\Delta \mb{y} _{t-p+1}’,D_ t]’\\ Z_{0} & =& [Z_{01}, \ldots , Z_{0T}]’ \\ Z_{1} & =& [Z_{11}, \ldots , Z_{1T}]’ \\ Z_{2} & =& [Z_{21}, \ldots , Z_{2T}]’ \end{eqnarray*}](images/etsug_varmax0806.png)
where 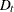 can be empty for Case 1, 1 for Case 3, and
can be empty for Case 1, 1 for Case 3, and  for Case 5.
for Case 5.
In Case 2,  and
and  are defined as
are defined as
![\begin{eqnarray*} Z_{1t}& =& [ \mb{y} _{t-1}’, 1]’ \\ Z_{2t}& =& [\Delta \mb{y} _{t-1}’,\ldots ,\Delta \mb{y} _{t-p+1}’]’\\ \end{eqnarray*}](images/etsug_varmax0810.png)
In Case 4,  and
and  are defined as
are defined as
![\begin{eqnarray*} Z_{1t}& =& [ \mb{y} _{t-1}’, t]’ \\ Z_{2t}& =& [\Delta \mb{y} _{t-1}’,\ldots ,\Delta \mb{y} _{t-p+1}’, 1]’\\ \end{eqnarray*}](images/etsug_varmax0811.png)
Let  be the matrix of parameters consisting of
be the matrix of parameters consisting of  , …,
, …,  , A, and
, A, and  , …,
, …,  , where parameter A corresponds with the regressors
, where parameter A corresponds with the regressors 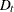 . Then the VECM(p) form is rewritten in these variables as
. Then the VECM(p) form is rewritten in these variables as
![\[ Z_{0t}=\balpha \bbeta ’ Z_{1t} +\Psi Z_{2t} +\bepsilon _ t \]](images/etsug_varmax0817.png)
The log-likelihood function is given by

The residuals, 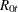 and
and 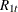 , are obtained by regressing
, are obtained by regressing  and
and  on
on  , respectively. The regression equation of residuals is
, respectively. The regression equation of residuals is
![\[ R_{0t} = \balpha \bbeta ’ R_{1t} + \hat{ \bepsilon }_ t \]](images/etsug_varmax0822.png)
The crossproducts matrices are computed
![\[ S_{ij} = \frac{1}{T}\sum _{t=1}^{T}R_{it}R_{jt}’,~ ~ i,j=0,1 \]](images/etsug_varmax0823.png)
Then the maximum likelihood estimator for 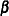 is obtained from the eigenvectors that correspond to the r largest eigenvalues of the following equation:
is obtained from the eigenvectors that correspond to the r largest eigenvalues of the following equation:
![\[ |\lambda S_{11} - S_{10}S_{00}^{-1}S_{01}| = 0 \]](images/etsug_varmax0824.png)
The eigenvalues of the preceding equation are squared canonical correlations between 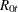 and
and 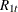 , and the eigenvectors that correspond to the r largest eigenvalues are the r linear combinations of
, and the eigenvectors that correspond to the r largest eigenvalues are the r linear combinations of 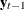 , which have the largest squared partial correlations with the stationary process
, which have the largest squared partial correlations with the stationary process  after correcting for lags and deterministic terms. Such an analysis calls for a reduced rank regression of
after correcting for lags and deterministic terms. Such an analysis calls for a reduced rank regression of  on
on 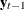 corrected for
corrected for  , as discussed by Anderson (1951). Johansen (1988) suggests two test statistics to test the null hypothesis that there are at most r cointegrating vectors
, as discussed by Anderson (1951). Johansen (1988) suggests two test statistics to test the null hypothesis that there are at most r cointegrating vectors
![\[ \mbox{H}_0: \lambda _ i=0 \mr{~ ~ for~ ~ } i=r+1,\ldots ,k \]](images/etsug_varmax0827.png)
Trace Test
The trace statistic for testing the null hypothesis that there are at most r cointegrating vectors is as follows:
![\[ \lambda _{trace} = -T\sum _{i=r+1}^{k}\log (1-\lambda _ i) \]](images/etsug_varmax0828.png)
The asymptotic distribution of this statistic is given by
![\[ tr\left\{ \int _0^1 (dW){\tilde W}’ \left(\int _0^1 {\tilde W}{\tilde W}’dr\right)^{-1}\int _0^1 {\tilde W}(dW)’ \right\} \]](images/etsug_varmax0829.png)
where  is the trace of a matrix A, W is the
is the trace of a matrix A, W is the 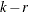 dimensional Brownian motion, and
dimensional Brownian motion, and  is the Brownian motion itself, or the demeaned or detrended Brownian motion according to the different specifications of
deterministic trends in the vector error correction model.
is the Brownian motion itself, or the demeaned or detrended Brownian motion according to the different specifications of
deterministic trends in the vector error correction model.
Maximum Eigenvalue Test
The maximum eigenvalue statistic for testing the null hypothesis that there are at most r cointegrating vectors is as follows:
![\[ \lambda _{max} = -T\log (1-\lambda _{r+1}) \]](images/etsug_varmax0832.png)
The asymptotic distribution of this statistic is given by
![\[ max\{ \int _0^1 (dW){\tilde W}’ (\int _0^1 {\tilde W}{\tilde W}’dr)^{-1}\int _0^1 {\tilde W}(dW)’ \} \]](images/etsug_varmax0833.png)
where  is the maximum eigenvalue of a matrix A. Osterwald-Lenum (1992) provided detailed tables of the critical values of these statistics.
is the maximum eigenvalue of a matrix A. Osterwald-Lenum (1992) provided detailed tables of the critical values of these statistics.
The following statements use the JOHANSEN option to compute the Johansen cointegration rank trace test of integrated order 1:
proc varmax data=simul2; model y1 y2 / p=2 cointtest=(johansen=(normalize=y1)); run;
Figure 42.68 shows the output based on the model specified in the MODEL statement. An intercept term is assumed. In the "Cointegration Rank Test Using Trace" table, the column Drift in ECM indicates that there is no separate drift in the error correction model, and the column Drift in Process indicates that the process has a constant drift before differencing. The "Cointegration Rank Test Using Trace" table shows the trace statistics and p-values based on Case 3, and the "Cointegration Rank Test Using Trace under Restriction" table shows the trace statistics and p-values based on Case 2. For a specified significance level, such as 5%, the output indicates that the null hypothesis that the series are not cointegrated (H0: Rank = 0) can be rejected, because the p-values for both Case 2 and Case 3 are less than 0.05. The output also shows that the null hypothesis that the series are cointegrated with rank 1 (H0: Rank = 1) cannot be rejected for either Case 2 or Case 3, because the p-values for these tests are both greater than 0.05.
Figure 42.68: Cointegration Rank Test (COINTTEST=(JOHANSEN=) Option)
| Cointegration Rank Test Using Trace | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | Pr > Trace | Drift in ECM | Drift in Process |
| 0 | 0 | 0.4644 | 61.7522 | <.0001 | Constant | Linear |
| 1 | 1 | 0.0056 | 0.5552 | 0.4559 | ||
| Cointegration Rank Test Using Trace Under Restriction | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | Pr > Trace | Drift in ECM | Drift in Process |
| 0 | 0 | 0.5209 | 76.3788 | <.0001 | Constant | Constant |
| 1 | 1 | 0.0426 | 4.2680 | 0.3741 | ||
Figure 42.69 shows which result, either Case 2 (the hypothesis H0) or Case 3 (the hypothesis H1), is appropriate depending on the significance level. Since the cointegration rank is chosen to be 1 by the result in Figure 42.68, look at the last row that corresponds to rank=1. Since the p-value is 0.054, the Case 2 cannot be rejected at the significance level 5%, but it can be rejected at the significance level 10%. For modeling of the two Case 2 and Case 3, see Figure 42.72 and Figure 42.73.
Figure 42.69: Cointegration Rank Test, Continued
Figure 42.70 shows the estimates of long-run parameter (Beta) and adjustment coefficients (Alpha) based on Case 3.
Figure 42.70: Cointegration Rank Test, Continued
Using the NORMALIZE= option, the first row of the "Beta" table has 1. Considering that the cointegration rank is 1, the long-run relationship of the series is
![\begin{eqnarray*} {\bbeta }’y_ t & =& \left[ \begin{array}{rr} 1 & -2.04869 \\ \end{array} \right] \left[ \begin{array}{r} y_1 \\ y_2 \\ \end{array} \right] \\ & =& y_{1t} - 2.04869 y_{2t} \\ y_{1t} & =& 2.04869 y_{2t} \end{eqnarray*}](images/etsug_varmax0835.png)
Figure 42.71 shows the estimates of long-run parameter (Beta) and adjustment coefficients (Alpha) based on Case 2.
Figure 42.71: Cointegration Rank Test, Continued
Considering that the cointegration rank is 1, the long-run relationship of the series is
![\begin{eqnarray*} {\bbeta }’y_ t & =& \left[ \begin{array}{rrr} 1 & -2.04366 & 6.75919 \\ \end{array} \right] \left[ \begin{array}{r} y_1 \\ y_2 \\ 1 \end{array} \right] \\ & =& y_{1t} - 2.04366~ y_{2t} + 6.75919 \\ y_{1t} & =& 2.04366~ y_{2t} - 6.75919 \end{eqnarray*}](images/etsug_varmax0836.png)
Estimation of Vector Error Correction Model
The preceding log-likelihood function is maximized for
![\begin{eqnarray*} \hat{\bbeta } & =& S_{11}^{-1/2} [v_1,\ldots ,v_ r] \\ \hat{\balpha } & =& S_{01}\hat{\bbeta }(\hat{\bbeta }’ S_{11}\hat{\bbeta })^{-1} \\ \hat\Pi & =& \hat{\balpha } \hat{\bbeta }’ \\ \hat\Psi ’ & =& (Z_{2}’Z_{2})^{-1} Z_{2}’(Z_{0} - Z_{1} \hat\Pi ’) \\ \hat\Sigma & =& (Z_{0} - Z_{2} \hat\Psi ’ - Z_{1} \hat\Pi ’)’ (Z_{0} - Z_{2} \hat\Psi ’ - Z_{1} \hat\Pi ’)/T \end{eqnarray*}](images/etsug_varmax0837.png)
The estimators of the orthogonal complements of  and
and 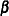 are
are
![\[ \hat{\bbeta }_{\bot } = S_{11} [v_{r+1},\ldots ,v_{k}] \]](images/etsug_varmax0838.png)
and
![\[ \hat{\balpha }_{\bot } = S_{00}^{-1} S_{01} [v_{r+1},\ldots ,v_{k}] \]](images/etsug_varmax0839.png)
Let  denote the parameter vector
denote the parameter vector  . The covariance of parameter estimates
. The covariance of parameter estimates  is obtained as the inverse of the negative Hessian matrix
is obtained as the inverse of the negative Hessian matrix  . Because
. Because  , the variance of
, the variance of  and the covariance between
and the covariance between  and
and  are calculated as follows:
are calculated as follows:
![\[ \mr{cov}(\mr{vec}(\hat{\Pi }), \mr{vec}(\hat{\Pi })) = (\hat{\bbeta } \otimes I_ k) \mr{cov}(\mr{vec}(\hat{\balpha }), \mr{vec}(\hat{\balpha })) (\hat{\bbeta } \otimes I_ k)’ \]](images/etsug_varmax0846.png)
![\[ \mr{cov}(\mr{vec}(\hat{\Pi }), \hat{\vartheta }) = (\hat{\bbeta } \otimes I_ k) \mr{cov}(\mr{vec}(\hat{\balpha }), \hat{\vartheta }) \]](images/etsug_varmax0847.png)
For Case 2 (Case 4), because the coefficient vector  (
( ) for the constant term (the linear trend term) is the product of
) for the constant term (the linear trend term) is the product of  and
and  (
( ), the variance of
), the variance of  (
( ) and the covariance between
) and the covariance between  (
( ) and
) and  are calculated as follows:
are calculated as follows:
![\[ \mr{cov}(\hat{\bdelta }_ i, \hat{\bdelta }_ i) = (\hat{\bbeta }_ i’ \otimes I_ k) \mr{cov}(\mr{vec}(\hat{\balpha }), \mr{vec}(\hat{\balpha })) (\hat{\bbeta }_ i’ \otimes I_ k)’,~ ~ i=0~ \mr{or}~ 1 \]](images/etsug_varmax0853.png)
![\[ \mr{cov}(\hat{\bdelta }_ i, \hat{\vartheta }) = (\hat{\bbeta }_ i’ \otimes I_ k) \mr{cov}(\mr{vec}(\hat{\balpha }), \hat{\vartheta }),~ ~ i=0~ \mr{or}~ 1 \]](images/etsug_varmax0854.png)
The following statements are examples of fitting the five different cases of the vector error correction models mentioned in the previous section.
For fitting Case 1,
model y1 y2 / p=2 noint; cointeg rank=1 normalize=y1;
For fitting Case 2,
model y1 y2 / p=2; cointeg rank=1 normalize=y1 ectrend;
For fitting Case 3,
model y1 y2 / p=2; cointeg rank=1 normalize=y1;
model y1 y2 / p=2 trend=linear; cointeg rank=1 normalize=y1 ectrend;
For fitting Case 5,
model y1 y2 / p=2 trend=linear; cointeg rank=1 normalize=y1;
In the previous example, the output from the COINTTEST=(JOHANSEN) option shown in Figure 42.69 indicates that you can fit the model by using either Case 2 or Case 3 because the test of the restriction was not significant at the 0.05 level, but was significant at the 0.10 level. Following both models are fit to show the differences in the displayed output. Figure 42.72 is for Case 2, and Figure 42.73 is for Case 3.
For Case 2,
proc varmax data=simul2; model y1 y2 / p=2 print=(estimates); cointeg rank=1 normalize=y1 ectrend; run;
Figure 42.72: Parameter Estimation with the ECTREND Option
| Parameter Alpha * Beta' Estimates | |||
|---|---|---|---|
| Variable | y1 | y2 | 1 |
| y1 | -0.48015 | 0.98126 | -3.24543 |
| y2 | 0.12538 | -0.25624 | 0.84748 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.72759 | -0.77463 |
| y2 | 0.38982 | -0.55173 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | -3.24543 | 0.33022 | -9.83 | <.0001 | 1, EC |
| AR1_1_1 | -0.48015 | 0.04886 | -9.83 | <.0001 | y1(t-1) | |
| AR1_1_2 | 0.98126 | 0.09984 | 9.83 | <.0001 | y2(t-1) | |
| AR2_1_1 | -0.72759 | 0.04623 | -15.74 | <.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.77463 | 0.04978 | -15.56 | <.0001 | D_y2(t-1) | |
| D_y2 | CONST2 | 0.84748 | 0.35394 | 2.39 | 0.0187 | 1, EC |
| AR1_2_1 | 0.12538 | 0.05236 | 2.39 | 0.0187 | y1(t-1) | |
| AR1_2_2 | -0.25624 | 0.10702 | -2.39 | 0.0187 | y2(t-1) | |
| AR2_2_1 | 0.38982 | 0.04955 | 7.87 | <.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.55173 | 0.05336 | -10.34 | <.0001 | D_y2(t-1) | |
Figure 42.72 can be reported as follows:
![\begin{eqnarray*} \Delta \mb{y} _ t & =& \left[ \begin{array}{rrr} -0.48015 & 0.98126 & -3.24543 \\ 0.12538 & -0.25624& 0.84748 \end{array} \right] \left[ \begin{array}{c} y_{1,t-1} \\ y_{2,t-1} \\ 1 \end{array} \right] \\ & & + \left[ \begin{array}{rr} -0.72759 & -0.77463 \\ 0.38982 & -0.55173 \end{array} \right] \Delta \mb{y} _{t-1} + \bepsilon _ t \end{eqnarray*}](images/etsug_varmax0855.png)
The keyword "EC" in the "Model Parameter Estimates" table means that the ECTREND option is used for fitting the model.
For fitting Case 3,
proc varmax data=simul2; model y1 y2 / p=2 print=(estimates); cointeg rank=1 normalize=y1; run;
Figure 42.73: Parameter Estimation without the ECTREND Option
| Parameter Alpha * Beta' Estimates | ||
|---|---|---|
| Variable | y1 | y2 |
| y1 | -0.46421 | 0.95103 |
| y2 | 0.17535 | -0.35923 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.74052 | -0.76305 |
| y2 | 0.34820 | -0.51194 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | -2.60825 | 1.32398 | -1.97 | 0.0518 | 1 |
| AR1_1_1 | -0.46421 | 0.05474 | -8.48 | <.0001 | y1(t-1) | |
| AR1_1_2 | 0.95103 | 0.11215 | 8.48 | <.0001 | y2(t-1) | |
| AR2_1_1 | -0.74052 | 0.05060 | -14.63 | <.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.76305 | 0.05352 | -14.26 | <.0001 | D_y2(t-1) | |
| D_y2 | CONST2 | 3.43005 | 1.39587 | 2.46 | 0.0159 | 1 |
| AR1_2_1 | 0.17535 | 0.05771 | 3.04 | 0.0031 | y1(t-1) | |
| AR1_2_2 | -0.35923 | 0.11824 | -3.04 | 0.0031 | y2(t-1) | |
| AR2_2_1 | 0.34820 | 0.05335 | 6.53 | <.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.51194 | 0.05643 | -9.07 | <.0001 | D_y2(t-1) | |
Figure 42.73 can be reported as follows:
![\begin{eqnarray*} \Delta \mb{y} _ t & =& \left[ \begin{array}{rr} -0.46421 & 0.95103 \\ 0.17535 & -0.35293 \end{array} \right] \mb{y} _{t-1} + \left[ \begin{array}{rr} -0.74052 & -0.76305 \\ 0.34820 & -0.51194 \end{array} \right] \Delta \mb{y} _{t-1} \\ & & + \left[ \begin{array}{r} -2.60825 \\ 3.43005 \end{array} \right] + \bepsilon _ t \end{eqnarray*}](images/etsug_varmax0856.png)
A Test for the Long-run Relations
Consider the example with the variables  log real money,
log real money,  log real income,
log real income,  deposit interest rate, and
deposit interest rate, and  bond interest rate. It seems a natural hypothesis that in the long-run relation, money and income have equal coefficients
with opposite signs. This can be formulated as the hypothesis that the cointegrated relation contains only
bond interest rate. It seems a natural hypothesis that in the long-run relation, money and income have equal coefficients
with opposite signs. This can be formulated as the hypothesis that the cointegrated relation contains only  and
and  through
through  . For the analysis, you can express these restrictions in the parameterization of
. For the analysis, you can express these restrictions in the parameterization of 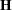 such that
such that  , where
, where 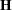 is a known
is a known  matrix and
matrix and  is the
is the  parameter matrix to be estimated. For this example,
parameter matrix to be estimated. For this example, 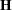 is given by
is given by
![\[ H = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \]](images/etsug_varmax0865.png)
Restriction 
When the linear restriction  is given, it implies that the same restrictions are imposed on all cointegrating vectors. You obtain the maximum likelihood
estimator of
is given, it implies that the same restrictions are imposed on all cointegrating vectors. You obtain the maximum likelihood
estimator of 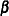 by reduced rank regression of
by reduced rank regression of  on
on  corrected for
corrected for  , solving the following equation
, solving the following equation

for the eigenvalues 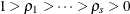 and eigenvectors
and eigenvectors  ,
,  given in the preceding section. Then choose
given in the preceding section. Then choose  that corresponds to the r largest eigenvalues, and the
that corresponds to the r largest eigenvalues, and the 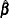 is
is  .
.
The test statistic for  is given by
is given by
![\[ T\sum _{i=1}^ r \log \{ (1-\rho _ i)/(1-\lambda _ i)\} \stackrel{d}{\rightarrow } \chi ^2_{r(k-s)} \]](images/etsug_varmax0875.png)
If the series has no deterministic trend, the constant term should be restricted by  as in Case 2. Then
as in Case 2. Then 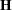 is given by
is given by
![\[ H = \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0\\ -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right] \]](images/etsug_varmax0877.png)
The following statements test that 2  :
:
proc varmax data=simul2; model y1 y2 / p=2; cointeg rank=1 h=(1,-2) normalize=y1; run;
Figure 42.74 shows the results of testing  . The input
. The input 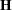 matrix is
matrix is  . The adjustment coefficient is reestimated under the restriction, and the test indicates that you cannot reject the null
hypothesis.
. The adjustment coefficient is reestimated under the restriction, and the test indicates that you cannot reject the null
hypothesis.
Figure 42.74: Testing of Linear Restriction (H= Option)
Test for the Weak Exogeneity and Restrictions of Alpha
Consider a vector error correction model:
![\[ \Delta \mb{y} _ t = \balpha \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb{y} _{t-i} + AD_ t + \bepsilon _ t \]](images/etsug_varmax0881.png)
Divide the process 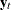 into
into  with dimension
with dimension 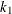 and
and 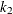 and the
and the 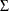 into
into
![\begin{eqnarray*} \Sigma = \left[ \begin{array}{cc} \Sigma _{11} & \Sigma _{12} \\ \Sigma _{21} & \Sigma _{22} \end{array} \right] \end{eqnarray*}](images/etsug_varmax0883.png)
Similarly, the parameters can be decomposed as follows:
![\begin{eqnarray*} \balpha = \left[ \begin{array}{c} \balpha _1 \\ \balpha _2 \end{array} \right] ~ ~ \Phi ^*_ i = \left[ \begin{array}{c} \Phi ^*_{1i} \\ \Phi ^*_{2i} \end{array} \right] ~ ~ A = \left[ \begin{array}{c} A_{1} \\ A_{2} \end{array} \right] \end{eqnarray*}](images/etsug_varmax0884.png)
Then the VECM(p) form can be rewritten by using the decomposed parameters and processes:
![\begin{eqnarray*} \left[ \begin{array}{c} \Delta \mb{y} _{1t} \\ \Delta \mb{y} _{2t} \end{array} \right] = \left[ \begin{array}{c} \balpha _1 \\ \balpha _2 \end{array} \right] \bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \left[ \begin{array}{c} \Phi ^*_{1i} \\ \Phi ^*_{2i} \end{array} \right] \Delta \mb{y} _{t-i} + \left[ \begin{array}{c} A_{1} \\ A_{2} \end{array} \right] D_ t + \left[ \begin{array}{c} \bepsilon _{1t} \\ \bepsilon _{2t} \end{array} \right] \end{eqnarray*}](images/etsug_varmax0885.png)
The conditional model for 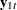 given
given 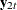 is
is

and the marginal model of 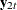 is
is
![\[ \Delta \mb{y} _{2t} =\alpha _2\bbeta ’\mb{y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^{*}_{2i}\Delta \mb{y} _{t-i} + A_2 D_ t + \bepsilon _{2t} \]](images/etsug_varmax0887.png)
where  .
.
The test of weak exogeneity of 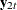 for the parameters
for the parameters  determines whether
determines whether  . Weak exogeneity means that there is no information about
. Weak exogeneity means that there is no information about 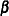 in the marginal model or that the variables
in the marginal model or that the variables 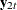 do not react to a disequilibrium.
do not react to a disequilibrium.
Restriction 
Consider the null hypothesis  , where J is a
, where J is a 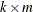 matrix with
matrix with  .
.
From the previous residual regression equation

you can obtain

where  and
and  is orthogonal to J such that
is orthogonal to J such that  .
.
Define
![\[ \Sigma _{JJ_{\bot }} = \bar{J}’\Sigma J_{\bot } \mr{~ ~ and~ ~ } \Sigma _{J_{\bot }J_{\bot }} = J_{\bot }’\Sigma J_{\bot } \]](images/etsug_varmax0899.png)
and let  . Then
. Then  can be written as
can be written as

Using the marginal distribution of  and the conditional distribution of
and the conditional distribution of  , the new residuals are computed as
, the new residuals are computed as

where
![\[ S_{JJ_{\bot }} = \bar{J}’S_{00}J_{\bot }, ~ ~ S_{J_{\bot }J_{\bot }} = J_{\bot }’S_{00}J_{\bot }, ~ ~ \mr{and ~ ~ } S_{J_{\bot }1} = J_{\bot }’S_{01} \]](images/etsug_varmax0905.png)
In terms of  and
and  , the MLE of
, the MLE of 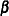 is computed by using the reduced rank regression. Let
is computed by using the reduced rank regression. Let
![\[ S_{ij\mb{.} J_{\bot }}=\frac{1}{T}\sum _{t=1}^{T}\tilde{{R}}_{it} \tilde{{R}}_{jt}’, \mr{~ ~ for~ ~ } i,j=1,J \]](images/etsug_varmax0908.png)
Under the null hypothesis  , the MLE
, the MLE 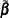 is computed by solving the equation
is computed by solving the equation

Then  , where the eigenvectors correspond to the r largest eigenvalues and are normalized such that
, where the eigenvectors correspond to the r largest eigenvalues and are normalized such that  ;
;  . The likelihood ratio test for
. The likelihood ratio test for  is
is
![\[ T\sum _{i=1}^ r\log \{ (1-\rho _ i)/(1-\lambda _ i)\} \stackrel{d}{\rightarrow } \chi ^2_{r(k-m)} \]](images/etsug_varmax0913.png)
See Theorem 6.1 in Johansen and Juselius (1990) for more details.
The test of weak exogeneity of 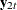 is a special case of the test
is a special case of the test  , considering
, considering  . Consider the previous example with four variables (
. Consider the previous example with four variables (  ). If
). If 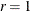 , you formulate the weak exogeneity of (
, you formulate the weak exogeneity of ( ) for
) for  as
as ![$J=[0, I_3]’$](images/etsug_varmax0918.png) and the weak exogeneity of
and the weak exogeneity of  for (
for ( ) as
) as ![$J = [I_3,0]’$](images/etsug_varmax0921.png) .
.
The following statements test the weak exogeneity of other variables, assuming 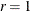 :
:
proc varmax data=simul2; model y1 y2 / p=2; cointeg rank=1 exogeneity normalize=y1; run;
Figure 42.75 shows that each variable is not the weak exogeneity of other variable.
Figure 42.75: Testing of Weak Exogeneity (EXOGENEITY Option)
General Tests and Restrictions on Parameters
The previous sections discuss some special forms of tests on 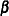 and
and  , namely the long-run relations that are expressed in the form
, namely the long-run relations that are expressed in the form  , the weak exogeneity test, and the null hypotheses on
, the weak exogeneity test, and the null hypotheses on  in the form
in the form  . In fact, with the help of the RESRICT and BOUND statements, you can estimate the models that have linear restrictions on
any parameters to be estimated, which means that you can implement the likelihood ratio (LR) test for any linear relationship
between the parameters.
. In fact, with the help of the RESRICT and BOUND statements, you can estimate the models that have linear restrictions on
any parameters to be estimated, which means that you can implement the likelihood ratio (LR) test for any linear relationship
between the parameters.
The restricted error correction model must be estimated through numerical optimization. You might need to use the NLOPTIONS
statement to try different options for the optimizer and the INITIAL statement to try different starting points. This is essentially
important because the  and
and 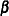 are usually not identifiable.
are usually not identifiable.
You can also use the TEST statement to apply the Wald test for any linear relationships between parameters that are not long-run
. Even more, you can test the constraints on 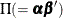 and
and  in Case 2 or
in Case 2 or  in Case 4 when the constant term or linear trend is restricted to the error correction term.
in Case 4 when the constant term or linear trend is restricted to the error correction term.
For more information and examples, see the section Analysis of Restricted Cointegrated Systems.
Forecasting of the VECM
Consider the cointegrated moving-average representation of the differenced process of 

Assume that  . The linear process
. The linear process 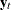 can be written as
can be written as

Therefore, for any  ,
,

The l-step-ahead forecast is derived from the preceding equation:

Note that
![\[ \lim _{l\rightarrow \infty } \bbeta ’\mb{y} _{t+l|t} = 0 \]](images/etsug_varmax0932.png)
since  and
and  . The long-run forecast of the cointegrated system shows that the cointegrated relationship holds, although there might exist
some deviations from the equilibrium status in the short-run. The covariance matrix of the predict error
. The long-run forecast of the cointegrated system shows that the cointegrated relationship holds, although there might exist
some deviations from the equilibrium status in the short-run. The covariance matrix of the predict error  is
is
![\[ \Sigma (l) = \sum _{i=1}^{l}[(\sum _{j=0}^{l-i}\Psi _ j)\Sigma (\sum _{j=0}^{l-i}\Psi _ j’)] \]](images/etsug_varmax0936.png)
When the linear process is represented as a VECM(p) model, you can obtain

The transition equation is defined as

where  is a state vector and the transition matrix is
is a state vector and the transition matrix is
![\begin{eqnarray*} F = \left[ \begin{array}{cccccc} I_ k & I_ k & 0 & \cdots & 0 \\ \Pi & (\Pi +\Phi ^*_1)& \Phi ^*_2 & \cdots & \Phi ^*_{p-1} \\ 0 & I_ k & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & I_ k & 0 \\ \end{array} \right] \end{eqnarray*}](images/etsug_varmax0940.png)
where 0 is a  zero matrix. The observation equation can be written
zero matrix. The observation equation can be written
![\[ \mb{y} _ t = \bdelta t + H \mb{z} _ t \]](images/etsug_varmax0942.png)
where ![$H=[I_ k,I_ k,0,\ldots ,0]$](images/etsug_varmax0943.png) .
.
The l-step-ahead forecast is computed as

Cointegration with Exogenous Variables
The error correction model with exogenous variables can be written as follows:
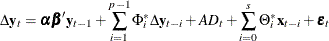
The following statements demonstrate how to fit VECMX(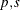 ), where
), where  and
and  from the P=2 and XLAG=1 options:
from the P=2 and XLAG=1 options:
proc varmax data=simul3; model y1 y2 = x1 / p=2 xlag=1; cointeg rank=1; run;
The following statements demonstrate how to BVECMX(2,1):
proc varmax data=simul3;
model y1 y2 = x1 / p=2 xlag=1
prior=(lambda=0.9 theta=0.1);
cointeg rank=1;
run;