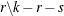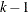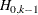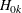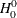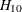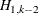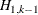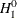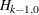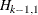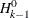The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
I(2) Model
The VARX(p,s) model can be written in the error correction form:
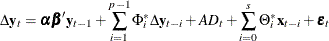
Let 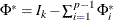 .
.
If  and
and  have full-rank r, and
have full-rank r, and 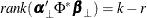 , then
, then  is an
is an  process.
process.
If the condition 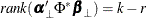 fails and
fails and 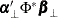 has reduced-rank
has reduced-rank 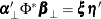 where
where 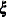 and
and 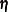 are
are 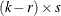 matrices with
matrices with 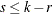 , then
, then 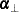 and
and 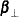 are defined as
are defined as 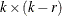 matrices of full rank such that
matrices of full rank such that 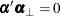 and
and 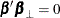 .
.
If 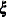 and
and 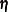 have full-rank s, then the process
have full-rank s, then the process 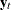 is
is 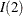 , which has the implication of
, which has the implication of 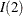 model for the moving-average representation.
model for the moving-average representation.
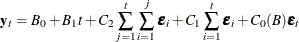
The matrices 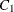 ,
, 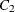 , and
, and 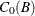 are determined by the cointegration properties of the process, and
are determined by the cointegration properties of the process, and 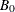 and
and 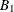 are determined by the initial values. For details, see Johansen (1995b).
are determined by the initial values. For details, see Johansen (1995b).
The implication of the 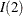 model for the autoregressive representation is given by
model for the autoregressive representation is given by
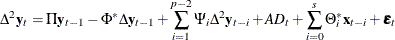
where 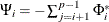 and
and 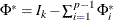 .
.
Test for I(2)
The 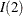 cointegrated model is given by the following parameter restrictions:
cointegrated model is given by the following parameter restrictions:
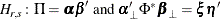
where 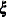 and
and 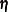 are
are 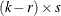 matrices with
matrices with 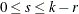 . Let
. Let 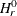 represent the
represent the 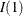 model where
model where  and
and  have full-rank r, let
have full-rank r, let 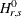 represent the
represent the 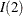 model where
model where 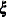 and
and 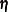 have full-rank s, and let
have full-rank s, and let 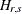 represent the
represent the 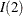 model where
model where 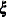 and
and 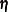 have rank
have rank 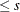 . The following table shows the relation between the
. The following table shows the relation between the 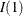 models and the
models and the 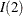 models.
models.
Table 42.6: Relation between the 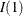 and
and 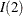 Models
Models
|
|
|
||||||||||
|
|
k |
|
|
1 |
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
|
|
|
= |
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
= |
|
Johansen (1995b) proposed the two-step procedure to analyze the 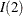 model. In the first step, the values of
model. In the first step, the values of 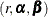 are estimated using the reduced rank regression analysis, performing the regression analysis
are estimated using the reduced rank regression analysis, performing the regression analysis 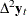 ,
, 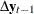 , and
, and 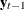 on
on 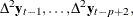 and
and 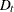 . This gives residuals
. This gives residuals 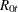 ,
, 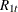 , and
, and 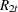 , and residual product moment matrices
, and residual product moment matrices
![\[ M_{ij} = \frac{1}{T} \sum _{t=1}^ TR_{it}R_{jt}’ ~ ~ \mr{for~ ~ } i,j=0,1,2 \]](images/etsug_varmax0986.png)
Perform the reduced rank regression analysis 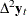 on
on 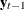 corrected for
corrected for 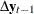 ,
, 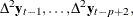 and
and 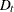 , and solve the eigenvalue problem of the equation
, and solve the eigenvalue problem of the equation
![\[ |\lambda M_{22\mb{.} 1} - M_{20\mb{.} 1}M_{00\mb{.} 1}^{-1}M_{02\mb{.} 1}| = 0 \]](images/etsug_varmax0987.png)
where 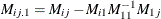 for
for 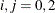 .
.
In the second step, if 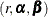 are known, the values of
are known, the values of 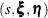 are determined using the reduced rank regression analysis, regressing
are determined using the reduced rank regression analysis, regressing 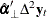 on
on 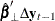 corrected for
corrected for 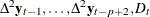 , and
, and 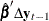 .
.
The reduced rank regression analysis reduces to the solution of an eigenvalue problem for the equation
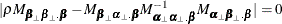
where
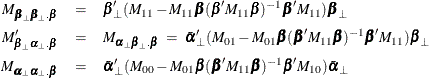
where 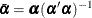 .
.
The solution gives eigenvalues 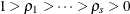 and eigenvectors
and eigenvectors 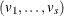 . Then, the ML estimators are
. Then, the ML estimators are
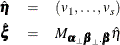
The likelihood ratio test for the reduced rank model 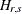 with rank
with rank 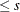 in the model
in the model 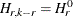 is given by
is given by
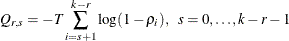
The following statements simulate an I(2) process and compute the rank test to test for cointegrated order 2:
proc iml;
alpha = { 1, 1}; * alphaOrthogonal = { 1, -1};
beta = { 1, -0.5}; * betaOrthogonal = { 1, 2};
* alphaOrthogonal' * phiStar * betaOrthogonal = 0;
phiStar = { 1 0, 0 0.5};
A1 = 2 * I(2) + alpha * beta` - phiStar;
A2 = phiStar - I(2);
phi = A1 // A2;
sig = I(2);
/* to simulate the vector time series */
call varmasim(y,phi) sigma=sig n=200 seed=2;
cn = {'y1' 'y2'};
create simul4 from y[colname=cn];
append from y;
close;
quit;
proc varmax data=simul4;
model y1 y2 /noint p=2 cointtest=(johansen=(iorder=2));
run;
The last two columns in Figure 42.76 explain the cointegration rank test with integrated order 1. For a specified significance level, such as 5%, the output indicates
that the null hypothesis that the series are not cointegrated (H0: 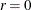 ) is rejected, because the p-value for this test, shown in the column Pr > Trace of I(1), is less than 0.05. The results also indicate that the null hypothesis
that there is a cointegrated relationship with cointegration rank 1 (H0:
) is rejected, because the p-value for this test, shown in the column Pr > Trace of I(1), is less than 0.05. The results also indicate that the null hypothesis
that there is a cointegrated relationship with cointegration rank 1 (H0: 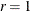 ) cannot be rejected at the 5% significance level, because the p-value for the test statistic, 0.7961, is greater than 0.05. Because of this latter result, the rows in the table that are
associated with
) cannot be rejected at the 5% significance level, because the p-value for the test statistic, 0.7961, is greater than 0.05. Because of this latter result, the rows in the table that are
associated with 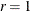 are further examined. The test statistic, 0.0257, tests the null hypothesis that the series are cointegrated order 2. The
p-value that is associated with this test is 0.8955, which indicates that the null hypothesis cannot be rejected at the 5%
significance level.
are further examined. The test statistic, 0.0257, tests the null hypothesis that the series are cointegrated order 2. The
p-value that is associated with this test is 0.8955, which indicates that the null hypothesis cannot be rejected at the 5%
significance level.
Figure 42.76: Cointegrated I(2) Test (IORDER= Option)