The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Multivariate GARCH Modeling
Stochastic volatility modeling is important in many areas, particularly in finance. To study the volatility of time series, GARCH models are widely used because they provide a good approach to conditional variance modeling.
BEKK Representation
Engle and Kroner (1995) propose a general multivariate GARCH model and call it a BEKK representation. Let  be the sigma field generated by the past values of
be the sigma field generated by the past values of 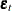 , and let
, and let 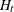 be the conditional covariance matrix of the k-dimensional random vector
be the conditional covariance matrix of the k-dimensional random vector 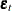 . Let
. Let 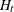 be measurable with respect to
be measurable with respect to  ; then the multivariate GARCH model can be written as
; then the multivariate GARCH model can be written as

where C,  and
and  are
are 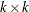 parameter matrices.
parameter matrices.
Consider the bivariate GARCH(1,1) model
![\begin{eqnarray*} H_ t & =& \left[ \begin{array}{cc} c_{11} & c_{12} \\ c_{12} & c_{22} \end{array} \right] +\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]’ \left[ \begin{array}{cc}\epsilon ^2_{1,t-1} & \epsilon _{1,t-1}\epsilon _{2,t-1} \\ \epsilon _{2,t-1}\epsilon _{1,t-1} & \epsilon ^2_{2,t-1} \end{array} \right] \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \\ & & + \left[ \begin{array}{cc} g_{11} & g_{12} \\ g_{21} & g_{22} \end{array} \right]’ H_{t-1}\left[ \begin{array}{cc} g_{11} & g_{12} \\ g_{21} & g_{22} \end{array} \right] \end{eqnarray*}](images/etsug_varmax1011.png)
or, representing the univariate model,

For the BEKK representation of the bivariate GARCH(1,1) model, the SAS statements are
model y1 y2; garch q=1 p=1 form=bekk;
The multistep forecast of the conditional covariance matrix,  , is obtained recursively through the formula
, is obtained recursively through the formula

where  for
for  .
.
CCC Representation
Bollerslev (1990) proposes a multivariate GARCH model with time-varying conditional variances and covariances but constant conditional correlations.
The conditional covariance matrix 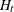 consists of
consists of

where 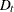 is a
is a  stochastic diagonal matrix with element
stochastic diagonal matrix with element  and S is a
and S is a  time-invariant correlation matrix with the typical element
time-invariant correlation matrix with the typical element  .
.
The element of 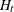 is
is

Note that  .
.
If you specify CORRCONSTANT=EXPECT, the element  of the time-invariant correlation matrix S is
of the time-invariant correlation matrix S is

where T is the sample size.
By default, or when you specify SUBFORM=GARCH,  follows a univariate GARCH process,
follows a univariate GARCH process,

As shown in many empirical studies, positive and negative innovations have different impacts on future volatility. There is a long list of variations of univariate GARCH models that consider the asymmetricity. Four typical variations follow:
For more information about the asymmetric GARCH models, see Engle and Ng (1993). You can choose the type of GARCH model of interest by specifying the SUBFORM= option.
The EGARCH model was proposed by Nelson (1991). Nelson and Cao (1992) argue that the nonnegativity constraints in the GARCH model are too restrictive. The GARCH model, implicitly or explicitly, imposes the nonnegative constraints on the parameters, whereas these parameters have no restrictions in the EGARCH model. In the EGARCH model, the conditional variance is an asymmetric function of lagged disturbances,

In the QGARCH model, the lagged errors’ centers are shifted from zero to some constant values,

In the TGARCH model, each lagged squared error has an extra slope coefficient,

where the indicator function  is one if
is one if  and zero otherwise.
and zero otherwise.
The PGARCH model not only considers the asymmetric effect but also provides a way to model the long memory property in the volatility,

where  and
and  .
.
Note that the implemented TGARCH model is also well known as GJR-GARCH (Glosten, Jaganathan, and Runkle 1993), which is similar to the threshold GARCH model proposed by Zakoian (1994) but not exactly the same. In Zakoian’s model, the conditional standard deviation is a linear function of the past values
of the white noise. Zakoian’s model can be regarded as a special case of the PGARCH model when  .
.
The following formulas are recursively implemented to obtain the multistep forecast of conditional error variance  and
and  :
:
-
for the GARCH(p, q) model:

-
for the EGARCH(p, q) model:

-
for the QGARCH(p, q) model:

-
for the TGARCH(p, q) model:

-
for the PGARCH(p, q) model:

In the preceding equations,  for
for  . Then, the multistep forecast of conditional covariance matrix
. Then, the multistep forecast of conditional covariance matrix  , is calculated by
, is calculated by

where  is the diagonal matrix with element
is the diagonal matrix with element  .
.
DCC Representation
Engle (2002) proposes a parsimonious parametric multivariate GARCH model that has time-varying conditional covariances and correlations.
The conditional covariance matrix 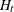 consists of
consists of

where 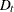 is a
is a  stochastic diagonal matrix with the element
stochastic diagonal matrix with the element  and
and  is a
is a  time-varying matrix with the typical element
time-varying matrix with the typical element  .
.
The element of 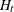 is
is

Note that  .
.
As in the CCC GARCH model, you can choose the type of GARCH model of interest by specifying the SUBFORM= option.
In the GARCH model,

In the EGARCH model, the conditional variance is an asymmetric function of lagged disturbances,

In the QGARCH model, the lagged errors’ centers are shifted from zero to some constant values,

In the TGARCH model, each lagged squared error has an extra slope coefficient,

where the indicator function  is one if
is one if  and zero otherwise.
and zero otherwise.
The PGARCH model not only considers the asymmetric effect but also provides another way to model the long memory property in the volatility,

where  and
and  .
.
The conditional correlation estimator  is
is

where  is the element of S, the unconditional correlation matrix.
is the element of S, the unconditional correlation matrix.
If you specify CORRCONSTANT=EXPECT, the element  of the unconditional correlation matrix S is
of the unconditional correlation matrix S is

where T is the sample size.
As shown in the CCC GARCH models, the following formulas are recursively implemented to obtain the multistep forecast of conditional
error variance  and
and  :
:
-
for the GARCH(p, q) model:

-
for the EGARCH(p, q) model:

-
for the QGARCH(p, q) model:

-
for the TGARCH(p, q) model:

-
for the PGARCH(p, q) model:

In the preceding equations,  for
for  . Then, the multistep forecast of conditional covariance matrix
. Then, the multistep forecast of conditional covariance matrix  , is calculated by
, is calculated by

where  is the diagonal matrix with element
is the diagonal matrix with element  , and
, and  is the matrix with element
is the matrix with element  ,
,

Estimation of GARCH Model
The log-likelihood function of the multivariate GARCH model is written without a constant term as
![\begin{eqnarray*} \ell = - \frac{1}{2}\sum _{t=1}^{T} [ \log |H_ t| + \bepsilon _{t}’H_ t^{-1}\bepsilon _{t} ] \end{eqnarray*}](images/etsug_varmax1058.png)
where 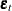 is calculated from the first-moment model (that is, the VARMAX model or VEC-ARMA model). The log-likelihood function is maximized
by an iterative numerical method such as quasi-Newton optimization. The starting values for the regression parameters are
obtained from the least squares estimates. The covariance of
is calculated from the first-moment model (that is, the VARMAX model or VEC-ARMA model). The log-likelihood function is maximized
by an iterative numerical method such as quasi-Newton optimization. The starting values for the regression parameters are
obtained from the least squares estimates. The covariance of 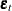 is used as the starting value for the GARCH constant parameters, and the starting values for the other GARCH parameters are
either
is used as the starting value for the GARCH constant parameters, and the starting values for the other GARCH parameters are
either  or
or  , depending on the GARCH model’s representation.
, depending on the GARCH model’s representation.
Prediction of Endogenous (Dependent) Variables
In multivariate GARCH models, the optimal (minimum MSE) l-step-ahead forecast of endogenous variables  uses the same formula as shown in the section Forecasting. However, the exogenous (independent) variables, if present, are always assumed to be nonstochastic (deterministic); that
is, to predict the endogenous variables, you must specify the future values of the exogenous variables. The prediction error
of the optimal l-step-ahead forecast is
uses the same formula as shown in the section Forecasting. However, the exogenous (independent) variables, if present, are always assumed to be nonstochastic (deterministic); that
is, to predict the endogenous variables, you must specify the future values of the exogenous variables. The prediction error
of the optimal l-step-ahead forecast is 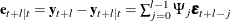 , with zero mean and covariance matrix,
, with zero mean and covariance matrix,
![\[ \Sigma _{t}(l) = \mr{Cov} (\mb{e} _{t+l|t} ) = \sum _{j=0}^{l-1}\Psi _{j} H_{t+l-j|t} \Psi _{j}’ \]](images/etsug_varmax1062.png)
where  is the h-step-ahead forecast of the conditional covariance matrix. As emphasized by the subscript t,
is the h-step-ahead forecast of the conditional covariance matrix. As emphasized by the subscript t,  is time-dependent. In the OUT= data set, the forecast standard errors and prediction intervals are constructed according
to
is time-dependent. In the OUT= data set, the forecast standard errors and prediction intervals are constructed according
to  . If you specify the COVPE option, the prediction error covariances that are output in the CovPredictError and CovPredictErrorbyVar
ODS tables are based on the time-independent formula
. If you specify the COVPE option, the prediction error covariances that are output in the CovPredictError and CovPredictErrorbyVar
ODS tables are based on the time-independent formula
![\[ \Sigma (l) = \sum _{j=0}^{l-1}\Psi _{j}\Sigma \Psi _{j}’ \]](images/etsug_varmax1065.png)
where 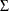 is the unconditional covariance matrix of innovations. The decomposition of the prediction error covariances is also based
on
is the unconditional covariance matrix of innovations. The decomposition of the prediction error covariances is also based
on 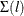 .
.
Covariance Stationarity
Define the multivariate GARCH process as
![\[ \mb{h} _ t = \sum _{i=1}^\infty G(B)^{i-1}[\mb{c} +A(B)\bm {\eta }_ t] \]](images/etsug_varmax1066.png)
where  ,
,  , and
, and  . This representation is equivalent to a GARCH(
. This representation is equivalent to a GARCH(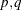 ) model by the following algebra:
) model by the following algebra:
![\begin{eqnarray*} \mb{h}_ t & =& \mb{c} + A(B)\bm {\eta }_ t + \sum _{i=2}^\infty G(B)^{i-1}[\mb{c} +A(B)\bm {\eta }_ t] \\ & =& \mb{c} + A(B)\bm {\eta }_ t + G(B)\sum _{i=1}^\infty G(B)^{i-1}[tmb{c} +A(B)\bm {\eta }_ t] \\ & =& \mb{c} + A(B)\bm {\eta }_ t + G(B) \mb{h}_ t \end{eqnarray*}](images/etsug_varmax1070.png)
Defining  and
and  gives a BEKK representation.
gives a BEKK representation.
The necessary and sufficient conditions for covariance stationarity of the multivariate GARCH process are that all the eigenvalues
of  are less than 1 in modulus.
are less than 1 in modulus.
An Example of a VAR(1)–ARCH(1) Model
The following DATA step simulates a bivariate vector time series to provide test data for the multivariate GARCH model:
data garch;
retain seed 16587;
esq1 = 0; esq2 = 0;
ly1 = 0; ly2 = 0;
do i = 1 to 1000;
ht = 6.25 + 0.5*esq1;
call rannor(seed,ehat);
e1 = sqrt(ht)*ehat;
ht = 1.25 + 0.7*esq2;
call rannor(seed,ehat);
e2 = sqrt(ht)*ehat;
y1 = 2 + 1.2*ly1 - 0.5*ly2 + e1;
y2 = 4 + 0.6*ly1 + 0.3*ly2 + e2;
if i>500 then output;
esq1 = e1*e1; esq2 = e2*e2;
ly1 = y1; ly2 = y2;
end;
keep y1 y2;
run;
The following statements fit a VAR(1)–ARCH(1) model to the data. For a VAR-ARCH model, you specify the order of the autoregressive model with the P=1 option in the MODEL statement and the Q=1 option in the GARCH statement. In order to produce the initial and final values of parameters, the TECH=QN option is specified in the NLOPTIONS statement.
proc varmax data=garch;
model y1 y2 / p=1
print=(roots estimates diagnose);
garch q=1;
nloptions tech=qn;
run;
Figure 42.77 through Figure 42.81 show the details of this example. Figure 42.77 shows the initial values of parameters.
Figure 42.77: Start Parameter Estimates for the VAR(1)–ARCH(1) Model
| Optimization Start | |||
|---|---|---|---|
| Parameter Estimates | |||
| N | Parameter | Estimate | Gradient Objective Function |
| 1 | CONST1 | 2.249575 | 0.000082533 |
| 2 | CONST2 | 3.902673 | 0.000401 |
| 3 | AR1_1_1 | 1.231775 | 0.000105 |
| 4 | AR1_2_1 | 0.576890 | -0.004811 |
| 5 | AR1_1_2 | -0.528405 | 0.000617 |
| 6 | AR1_2_2 | 0.343714 | 0.001811 |
| 7 | GCHC1_1 | 9.929763 | 0.151293 |
| 8 | GCHC1_2 | 0.193163 | -0.014305 |
| 9 | GCHC2_2 | 4.063245 | 0.370333 |
| 10 | ACH1_1_1 | 0.001000 | -0.667182 |
| 11 | ACH1_2_1 | 0 | -0.068905 |
| 12 | ACH1_1_2 | 0 | -0.734486 |
| 13 | ACH1_2_2 | 0.001000 | -3.127035 |
Figure 42.78 shows the final parameter estimates.
Figure 42.78: Results of Parameter Estimates for the VAR(1)–ARCH(1) Model
| Optimization Results | |||
|---|---|---|---|
| Parameter Estimates | |||
| N | Parameter | Estimate | Gradient Objective Function |
| 1 | CONST1 | 2.156865 | 0.000246 |
| 2 | CONST2 | 4.048879 | 0.000105 |
| 3 | AR1_1_1 | 1.224620 | -0.001957 |
| 4 | AR1_2_1 | 0.609651 | 0.000173 |
| 5 | AR1_1_2 | -0.534248 | -0.000468 |
| 6 | AR1_2_2 | 0.302599 | -0.000375 |
| 7 | GCHC1_1 | 8.238625 | -0.000056090 |
| 8 | GCHC1_2 | -0.231183 | -0.000021724 |
| 9 | GCHC2_2 | 1.565459 | 0.000110 |
| 10 | ACH1_1_1 | 0.374255 | -0.000419 |
| 11 | ACH1_2_1 | 0.035883 | -0.000606 |
| 12 | ACH1_1_2 | 0.057461 | 0.001636 |
| 13 | ACH1_2_2 | 0.717897 | -0.000149 |
Figure 42.79 shows the conditional variance by using the BEKK representation of the ARCH(1) model. The ARCH parameters are estimated as follows by the vectorized parameter matrices:
![\begin{eqnarray*} \bepsilon _ t|\mathcal{F}(t-1) & \sim & N(0,H_ t) \\ H_ t & = & \left[ \begin{matrix} 8.23863 & -0.23118 \\ -0.23118 & 1.56546 \\ \end{matrix} \right] \\ & + & \left[ \begin{matrix} 0.37426 & 0.05746 \\ 0.03588 & 0.71790 \\ \end{matrix} \right]’ \bepsilon _{t-1}\bepsilon _{t-1}’ \left[ \begin{matrix} 0.37426 & 0.05746 \\ 0.03588 & 0.71790 \\ \end{matrix} \right] \end{eqnarray*}](images/etsug_varmax1074.png)
Figure 42.79: ARCH(1) Parameter Estimates for the VAR(1)–ARCH(1) Model
| Type of Model | VAR(1)-ARCH(1) |
|---|---|
| Estimation Method | Maximum Likelihood Estimation |
| Representation Type | BEKK |
| GARCH Model Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
t Value | Pr > |t| |
| GCHC1_1 | 8.23863 | 0.72663 | 11.34 | 0.0001 |
| GCHC1_2 | -0.23118 | 0.21434 | -1.08 | 0.2813 |
| GCHC2_2 | 1.56546 | 0.19407 | 8.07 | 0.0001 |
| ACH1_1_1 | 0.37426 | 0.07502 | 4.99 | 0.0001 |
| ACH1_2_1 | 0.03588 | 0.06974 | 0.51 | 0.6071 |
| ACH1_1_2 | 0.05746 | 0.02597 | 2.21 | 0.0274 |
| ACH1_2_2 | 0.71790 | 0.06895 | 10.41 | 0.0001 |
Figure 42.80 shows the AR parameter estimates and their significance.
The fitted VAR(1) model with the previous conditional covariance ARCH model is written as follows:
![\[ \mb{y} _ t = \left[ \begin{matrix} 2.15687 \\ 4.04888 \\ \end{matrix} \right] + \left[ \begin{matrix} 1.22462 & -0.53425 \\ 0.60965 & 0.30260 \\ \end{matrix} \right] \mb{y} _{t-1} + \bepsilon _ t \]](images/etsug_varmax1075.png)
Figure 42.80: VAR(1) Parameter Estimates for the VAR(1)–ARCH(1) Model
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| y1 | CONST1 | 2.15687 | 0.21717 | 9.93 | 0.0001 | 1 |
| AR1_1_1 | 1.22462 | 0.02542 | 48.17 | 0.0001 | y1(t-1) | |
| AR1_1_2 | -0.53425 | 0.02807 | -19.03 | 0.0001 | y2(t-1) | |
| y2 | CONST2 | 4.04888 | 0.10663 | 37.97 | 0.0001 | 1 |
| AR1_2_1 | 0.60965 | 0.01216 | 50.13 | 0.0001 | y1(t-1) | |
| AR1_2_2 | 0.30260 | 0.01491 | 20.30 | 0.0001 | y2(t-1) | |
Figure 42.81 shows the roots of the AR and ARCH characteristic polynomials. The eigenvalues have a modulus less than one.
Figure 42.81: Roots for the VAR(1)–ARCH(1) Model
| Roots of AR Characteristic Polynomial | |||||
|---|---|---|---|---|---|
| Index | Real | Imaginary | Modulus | Radian | Degree |
| 1 | 0.76361 | 0.33641 | 0.8344 | 0.4150 | 23.7762 |
| 2 | 0.76361 | -0.33641 | 0.8344 | -0.4150 | -23.7762 |
| Roots of GARCH Characteristic Polynomial | |||||
|---|---|---|---|---|---|
| Index | Real | Imaginary | Modulus | Radian | Degree |
| 1 | 0.52388 | 0.00000 | 0.5239 | 0.0000 | 0.0000 |
| 2 | 0.26661 | 0.00000 | 0.2666 | 0.0000 | 0.0000 |
| 3 | 0.26661 | 0.00000 | 0.2666 | 0.0000 | 0.0000 |
| 4 | 0.13569 | 0.00000 | 0.1357 | 0.0000 | 0.0000 |