The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Example 42.3 Analysis of Restricted Cointegrated Systems
The structural relationships between economic time series have been of interest for decades. Because of the cointegration, the vector error correction model (VECM), introduced by Engle and Granger (1987), is one of the most important tools for performing such analysis. Although there exist analytical solutions for a nonrestricted VECM and some restricted VECMs in special forms, the estimation of a generally restricted VECM relies on numerical methods. This section illustrates how to use the RESTRICT (or BOUND) and TEST statements, together with the COINTEG statement, to estimate the restricted VECM and perform the statistical tests. For more information about this topic, see Boswijk and Doornik (2004) and references therein.
The data are simulated based on the VECM
![\begin{eqnarray*} \Delta \mb{y} _ t & =& \balpha \bbeta ’\mb{y}_{t-1}+\Phi _1^*\Delta \mb{y}_{t-1} +\Theta _0^*\mb{x}_{t}+ \bepsilon _ t \\ & =& \left[ \begin{array}{rr} 0.01 & -0.02 \\ -0.03 & 0.04 \\ 0.05 & -0.06 \\ 0 & 0 \end{array} \right] \left[ \begin{array}{rrrr} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{array} \right] \mb{y}_{t-1} \\ & & + \left[ \begin{array}{rrrr} -0.01 & 0.03 & 0.05 & -0.02 \\ 0.02 & -0.04 & 0.06 & 0.03 \\ 0 & 0 & 0.10 & 0 \\ 0 & 0 & 0 & 0.04 \end{array} \right] \Delta \mb{y}_{t-1} + \left[ \begin{array}{r} 0 \\ 0 \\ 0 \\ 0 \end{array} \right] \mb{x}_{t} + \bepsilon _ t, \\ \bepsilon _ t & \sim & \mr{i.i.d.}~ N(0,\Sigma ),\Sigma =I_4 \end{eqnarray*}](images/etsug_varmax1158.png)
where 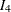 is the
is the 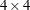 identity matrix.
identity matrix.
The following statements implement the simulation:
title 'Analysis of Restricted Cointegrated Systems';
proc iml;
alpha = {0.01 -0.02, -0.03 0.04, 0.05 -0.06, 0 0};
beta = {1 0, 0 1, -1 0, 0 -1};
phiStar = {-0.01 0.03 0.05 -0.02,
0.02 -0.04 0.06 0.03,
0 0 0.10 0,
0 0 0 0.04};
Pi = alpha * beta` ;
A1 = I(4) + Pi+ phiStar;
A2 = -phiStar;
phi = A1 // A2;
sig = I(4);
/* to simulate the vector time series */
T = 600;
myseed = 2;
call varmasim(y,phi) sigma=sig n=T seed=myseed;
x = J(T,1,0);
do i = 1 to T;
x[i] = normal(myseed);
end;
y = y || x;
cn = {'y1' 'y2' 'y3' 'y4' 'x'};
create simul5 from y[colname=cn];
append from y;
close;
quit;
Weak Exogeneity Tests
This example shows different methods for checking weak exogeneity.
The first method uses the EXOGENEITY option in the following statements, and the test results are shown in Output 42.3.1.
/* Method 1 -- To use the EXOGENEITY option */ ods output LogLikelihood = tbl_ll_g; proc varmax data=simul5; model y1 y2 y3 y4 = x / noint p=2; cointeg rank=2 exogeneity; run;
Output 42.3.1: Test Weak Exogeneity with the EXOGENEITY Option
The second method uses the RESTRICT statement and then the likelihood ratio (LR) test in the following statements. The results
are shown in Output 42.3.2. In theory, the first and second methods should have exactly same statistics and p-values because they implement the same LR tests. However, because of the difference between the analytical solution and the
numerical solution for the restricted VECM, the statistics are a little different, although for the 0.05 significance level
they lead to the same correct conclusion: the variable 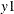 is not the weak exogeneity of variables
is not the weak exogeneity of variables 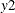 ,
, 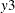 , and
, and 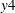 ; the variable
; the variable 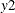 is not the weak exogeneity of variables
is not the weak exogeneity of variables 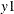 ,
, 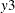 , and
, and 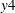 ; the variable
; the variable 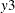 is not the weak exogeneity of variables
is not the weak exogeneity of variables 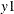 ,
, 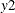 , and
, and 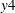 ; the variable
; the variable 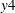 is the weak exogeneity of variables
is the weak exogeneity of variables 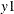 ,
, 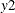 , and
, and 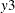 .
.
/* Method 2 -- Use the RESTRICT statement and implement LR test */
%macro LRTestForVECM();
%do i = 1 %to 4;
ods output LogLikelihood = tbl_ll_r1_&i.;
proc varmax data=simul5;
model y1 y2 y3 y4 = x / noint p=2;
cointeg rank=2;
restrict alpha(&i.,1:2) = 0;
run;
%end;
proc iml;
use tbl_ll_g;
read all var {nValue1} into ll_g;
close;
%do i = 1 %to 4;
use tbl_ll_r1_&i.;
read all var {nValue1} into ll_r_&i.;
close;
%end;
DF = J(4,1,2);
ll_r = ll_r_1 // ll_r_2 // ll_r_3 // ll_r_4;
Stat = -2*(ll_r - ll_g);
pValue = 1-cdf("CHISQUARE", Stat, DF);
Test = {"H0: Alpha(1,)=0"} // {"H0: Alpha(2,)=0"}
// {"H0: Alpha(3,)=0"} // {"H0: Alpha(4,)=0"};
print Test DF Stat pValue;
quit;
%mend;
%LRTestForVECM();
Output 42.3.2: Test Weak Exogeneity with the RESTRICT Statement and LR Tests
The third method uses the TEST statement, which implements the Wald tests. Asymptotically, the Wald test has the same distribution as the LR test.
/* Method 3 -- To use the TEST statement and the Wald test */ proc varmax data=simul5; model y1 y2 y3 y4 = x / noint p=2; cointeg rank=2; test alpha(1,1:2) = 0; test alpha(2,1:2) = 0; test alpha(3,1:2) = 0; test alpha(4,1:2) = 0; run;
Based on the test results shown in Output 42.3.3, the same correct conclusion can be obtained at the 0.05 significance level: the variable 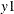 is not the weak exogeneity of variables
is not the weak exogeneity of variables 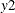 ,
, 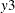 , and
, and 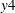 ; the variable
; the variable 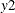 is not the weak exogeneity of variables
is not the weak exogeneity of variables 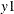 ,
, 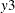 , and
, and 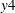 ; the variable
; the variable 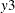 is not the weak exogeneity of variables
is not the weak exogeneity of variables 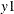 ,
, 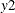 , and
, and 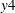 ; the variable
; the variable 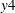 is the weak exogeneity of variables
is the weak exogeneity of variables 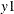 ,
, 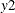 , and
, and 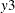 .
.
Output 42.3.3: Test Weak Exogeneity with the TEST Statement, Wald Tests
Identification
This example shows how important it is to identify  and
and  when applying the Wald test on
when applying the Wald test on  . First, in the following statements, there are no constraints on
. First, in the following statements, there are no constraints on  :
:
proc varmax data=simul5; model y1 y2 y3 y4 = x / noint p=2; cointeg rank=2; test alpha(1,2) = alpha(2,2) + alpha(3,2); run;
As shown in Output 42.3.4, based on the test results, the null hypothesis H0: ![$\balpha [1,2] = \balpha [2,2] + \balpha [3,2]$](images/etsug_varmax1161.png) should be rejected at the 0.05 significance level, although the true parameter values for the data generating process indicate
that H0 is correct.
should be rejected at the 0.05 significance level, although the true parameter values for the data generating process indicate
that H0 is correct.
Output 42.3.4: Importance of Identifying  and
and  in the Wald Test
in the Wald Test
In the following statements, 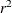 constraints are now imposed on
constraints are now imposed on  , where r is the cointegration rank:
, where r is the cointegration rank:
proc varmax data=simul5; model y1 y2 y3 y4 = x / noint p=2; cointeg rank=2; restrict beta(3:4,1:2) = -I(2); test alpha(1,2) = alpha(2,2) + alpha(3,2); run;
As shown in Output 42.3.5, the null hypothesis cannot be rejected at 0.05 significance level; that is to say, the correct conclusion is achieved.
Output 42.3.5: Importance of Identifying  and
and  in the Wald Test, Continued
in the Wald Test, Continued
Besides  , other short-run parameters in a VECM can also be tested by using the TEST statement. Because short-run parameters other
than
, other short-run parameters in a VECM can also be tested by using the TEST statement. Because short-run parameters other
than  are identified in a VECM, it is not necessary to impose additional constraints on
are identified in a VECM, it is not necessary to impose additional constraints on  and
and  . The following statements test the null hypothesis H0:
. The following statements test the null hypothesis H0: 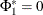 :
:
proc varmax data=simul5; model y1 y2 y3 y4 = x / noint p=2; cointeg rank=2; test ar(2); run;
According to the results shown in Output 42.3.6, the null hypothesis should be rejected at the 0.05 significance level.
Output 42.3.6: Wald Tests for Short-Run Parameters
The following statements test the null hypothesis H0: 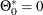 :
:
proc varmax data=simul5; model y1 y2 y3 y4 = x / noint p=2; cointeg rank=2; test xl; run;
According to the results shown in Output 42.3.7, the null hypothesis cannot be rejected at the 0.05 significance level.
Output 42.3.7: Wald Tests for Short-Run Parameters, Continued
Besides the parameters that are estimated in a VECM, you can also use the TEST statement on 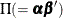 , and
, and 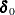 or
or 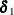 for Case 2 or 4 when the constant or linear trend, respectively, is restricted in the error correction term. However, keep
in mind that the covariance matrix for these parameter estimates is singular when the cointegration rank is less than the
number of dependent variables; hence, you might not get the results for some tests.
for Case 2 or 4 when the constant or linear trend, respectively, is restricted in the error correction term. However, keep
in mind that the covariance matrix for these parameter estimates is singular when the cointegration rank is less than the
number of dependent variables; hence, you might not get the results for some tests.
proc varmax data=simul5;
model y1 y2 y3 y4 = x / noint p=2;
cointeg rank=2;
test ar(1,4,1:4);
test ar(1,4,{1 3});
run;
As shown in Output 42.3.8, the first test on H0: ![$\Pi [4,]=0$](images/etsug_varmax1167.png) cannot be calculated, whereas the second test on H0:
cannot be calculated, whereas the second test on H0: ![$\Pi [4,1] = \Pi [4,3] = 0$](images/etsug_varmax1168.png) can be.
can be.
Output 42.3.8: Wald Tests for 
Tests for Long-Run Parameter
This example focuses on testing the relationships on the long-run parameter  . Here, only the following specific form of hypothesis is discussed,
. Here, only the following specific form of hypothesis is discussed,
![\[ \mr{H0}\colon \bbeta = (\bH , \bphi ) \]](images/etsug_varmax1169.png)
where 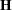 is a known
is a known 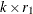 matrix,
matrix, 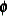 is a freely varying
is a freely varying 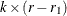 parameter matrix, k is the number of dependent variables, r is the cointegration rank, and
parameter matrix, k is the number of dependent variables, r is the cointegration rank, and 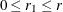 . Other forms of hypothesis—for example, H0:
. Other forms of hypothesis—for example, H0: 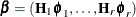 or H0:
or H0: 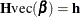 —are omitted, although they can also be implemented in the same logic. The following statements test the null hypothesis that
—are omitted, although they can also be implemented in the same logic. The following statements test the null hypothesis that
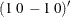 is in the cointegrating space that is spanned by
is in the cointegrating space that is spanned by  :
:
/* Use the RESTRICT statement and LR test for restrictions on Beta. */
/* H0: Beta = [ H, phi ] where H is known and phi is free */
ods output LogLikelihood = tbl_ll_r2;
proc varmax data=simul5;
model y1 y2 y3 y4 = x / noint p=2;
cointeg rank=2;
restrict beta(,1) = {1, 0, -1, 0};
nloptions tech=qn maxit=5000;
run;
proc iml;
use tbl_ll_g;
read all var {nValue1} into ll_g;
close;
use tbl_ll_r2;
read all var {nValue1} into ll_r;
close;
DF = (4-2)*1; /* DF = (k-r)*r_1 */
Stat = -2*(ll_r - ll_g);
pValue = 1-cdf("CHISQUARE", stat, df);
Test = "H0: Beta[1,1:4] = {1 0 -1 0}'";
print Test DF Stat pValue;
quit;
According to the result shown in Output 42.3.9, the null hypothesis cannot be rejected at the 0.05 significance level.
Output 42.3.9: LR Tests on Long-Run Parameter 
The following statements test the null hypothesis that the cointegrating space is spanned by
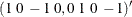 :
:
/* H0: Beta = H, where H is the true Beta for DGP */
ods output LogLikelihood = tbl_ll_r3;
proc varmax data=simul5;
model y1 y2 y3 y4 = x / noint p=2;
cointeg rank=2;
restrict beta = I(2) // (-I(2));
nloptions tech=qn maxit=5000;
run;
proc iml;
use tbl_ll_g;
read all var {nValue1} into ll_g;
close;
use tbl_ll_r3;
read all var {nValue1} into ll_r;
close;
DF = (4-2)*2; /* DF = (k-r)*r_1 */
Stat = -2*(ll_r - ll_g);
pValue = 1-cdf("CHISQUARE", stat, df);
Test = "H0: Beta = {1 0, 0 1, -1 0, 0 -1}";
print Test DF Stat pValue;
quit;
According to the result shown in Output 42.3.10, the null hypothesis cannot be rejected at the 0.05 significance level.
Output 42.3.10: LR Tests on Long-Run Parameter  , Continued
, Continued
The following statements test the null hypothesis that the cointegrating space is spanned by 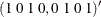 , the orthogonal matrix to the true
, the orthogonal matrix to the true  for the data generating process:
for the data generating process:
/* H0: Beta = H, where H is the matrix orthogonal
to the true Beta for DGP */
ods output LogLikelihood = tbl_ll_r4;
proc varmax data=simul5;
model y1 y2 y3 y4 = x / noint p=2;
cointeg rank=2;
restrict beta = {1 0, 0 1, 1 0, 0 1};
nloptions tech=qn maxit=5000;
run;
proc iml;
use tbl_ll_g;
read all var {nValue1} into ll_g;
close;
use tbl_ll_r4;
read all var {nValue1} into ll_r;
close;
DF = (4-2)*2; /* DF = (k-r)*r_1 */
Stat = -2*(ll_r - ll_g);
pValue = 1-cdf("CHISQUARE", stat, df);
Test = "H0: Beta = {1 0, 0 1, 1 0, 0 1}";
print Test DF Stat pValue;
quit;
According to the result shown in Output 42.3.11, the null hypothesis should be rejected at the 0.05 significance level.
Output 42.3.11: LR Tests on Long-Run Parameter  , Continued
, Continued
For the VECM, the BOUND statement can be regarded as an alias of the RESTRICT statement; that is, you can directly replace any RESTRICT statement with a BOUND statement and get the same result. The linear inequality constraints in the restricted cointegrated systems are not discussed in this section, although they are also supported in the BOUND and RESTRICT statements. For more information, see the sections BOUND Statement and RESTRICT Statement.
Obtaining the numerical solution for the restricted VECM is not an easy task in most cases. You might need to use the INITIAL and NLOPTIONS statements to tune the process. For more information, see the sections INITIAL Statement and NLOPTIONS Statement.