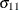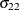The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
OUTSTAT= Data Set
The OUTSTAT= data set contains estimation results of the fitted model produced by the VARMAX statement. The following output
variables can be created. The subindex i is  , where k is the number of endogenous variables.
, where k is the number of endogenous variables.
-
the BY variables
-
NAME, a character variable that contains the name of endogenous (dependent) variables
-
SIGMA
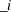 , numeric variables that contain the estimate of the innovation covariance matrix
, numeric variables that contain the estimate of the innovation covariance matrix
-
AICC, a numeric variable that contains the corrected Akaike’s information criterion value
-
HQC, a numeric variable that contains the Hannan-Quinn’s information criterion value
-
AIC, a numeric variable that contains the Akaike’s information criterion value
-
SBC, a numeric variable that contains the Schwarz Bayesian’s information criterion value
-
FPEC, a numeric variable that contains the final prediction error criterion value
-
FValue, a numeric variable that contains the F statistics
-
PValue, a numeric variable that contains p-value for the F statistics
If the JOHANSEN= option is specified, the following items are added:
-
Eigenvalue, a numeric variable that contains eigenvalues for the cointegration rank test of integrated order 1
-
RestrictedEigenvalue, a numeric variable that contains eigenvalues for the cointegration rank test of integrated order 1 when the NOINT option is not specified
-
Beta
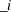 , numeric variables that contain long-run effect parameter estimates,
, numeric variables that contain long-run effect parameter estimates, 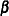
-
Alpha
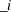 , numeric variables that contain adjustment parameter estimates,
, numeric variables that contain adjustment parameter estimates, 
If the JOHANSEN=(IORDER=2) option is specified, the following items are added:
-
EValueI2
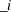 , numeric variables that contain eigenvalues for the cointegration rank test of integrated order 2
, numeric variables that contain eigenvalues for the cointegration rank test of integrated order 2
-
EValueI1, a numeric variable that contains eigenvalues for the cointegration rank test of integrated order 1
-
Eta
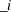 , numeric variables that contain the parameter estimates in integrated order 2,
, numeric variables that contain the parameter estimates in integrated order 2, 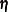
-
Xi
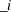 , numeric variables that contain the parameter estimates in integrated order 2,
, numeric variables that contain the parameter estimates in integrated order 2, 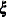
The OUTSTAT= data set contains the values shown Table 42.11 for a bivariate case.
Table 42.11: OUTSTAT= Data Set
|
Obs |
NAME |
SIGMA_1 |
SIGMA_2 |
AICC |
RSquare |
FValue |
PValue |
|
1 |
y1 |
|
|
|
|
|
|
|
2 |
y2 |
|
|
. |
|
|
|
|
Obs |
EValueI2_1 |
EValueI2_2 |
EValueI1 |
Beta_1 |
Beta_2 |
|
1 |
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
Obs |
Alpha_1 |
Alpha_2 |
Eta_1 |
Eta_2 |
Xi_1 |
Xi_2 |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Consider the following example:
proc varmax data=simul2 outstat=stat;
model y1 y2 / p=2 noint noprint
cointtest=(johansen=(iorder=2));
cointeg rank=1 normalize=y1;
run;
proc print data=stat;
run;
The output in Figure 42.88 shows the results of the OUTSTAT= data set.
Figure 42.88: OUTSTAT= Data Set
| Obs | NAME | SIGMA_1 | SIGMA_2 | AICC | HQC | AIC | SBC | FPEC | RSquare | FValue | PValue | EValueI2_1 | EValueI2_2 | EValueI1 | Beta_1 | Beta_2 | Alpha_1 | Alpha_2 | Eta_1 | Eta_2 | Xi_1 | Xi_2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | y1 | 94.7557 | 4.527 | 9.37221 | 9.43236 | 9.36834 | 9.52661 | 11712.14 | 0.93900 | 482.308 | 6.1637E-57 | 0.98486 | 0.95079 | 0.50864 | 1.00000 | 1.00000 | -0.46680 | 0.007937 | -0.012307 | 0.027030 | 54.1606 | -52.3144 |
| 2 | y2 | 4.5268 | 109.570 | . | . | . | . | . | 0.93912 | 483.334 | 5.6124E-57 | 0.81451 | . | 0.01108 | -1.95575 | -1.33622 | 0.10667 | 0.033530 | 0.015555 | 0.023086 | -79.4240 | -18.3308 |