The MI Procedure

FCS Statement

FCS <options>;

The FCS statement specifies a multivariate imputation by fully conditional specification methods. If you specify an FCS statement, you must also specify a VAR statement.

Table 75.2 summarizes the options available for the FCS statement.

Table 75.2: Summary of Options in FCS

Option	Description
Imputation Details
NBITER=	Specifies the number of burn-in iterations
Data Set
OUTITER=	Outputs parameter estimates used in iterations
ODS Graphics Output
PLOTS=TRACE	Displays trace plots
Imputation Methods
DISCRIM	Specifies the discriminant function method
LOGISTIC	Specifies the logistic regression method
REG	Specifies the regression method
REGPMM	Specifies the predictive mean matching method

The following options are available for the FCS statement in addition to the imputation methods specified (in alphabetical order):

NBITER=number

specifies the number of burn-in iterations before each imputation. The default is NBITER=20.

OUTITER <( options )> =SAS-data-set

creates an output SAS data set of TYPE=COV that contains parameters used in the imputation step for each iteration. The data set includes variables named _Imputation_ and _Iteration_ to identify the imputation number and iteration number.

The parameters in the output data set depend on the options specified. You can specify the options MEAN and STD to output parameters of means and standard deviations, respectively. When no options are specified, the output data set contains the mean parameters used in the imputation step for each iteration. See the section Output Data Sets for a description of this data set.

PLOTS <( LOG )> <= TRACE < ( trace-options ) >>

requests statistical graphics of trace plots from iterations via the Output Delivery System (ODS).

ODS Graphics must be enabled before plots can be requested. For example:

ods graphics on;
proc mi data=Fitness1 seed=501213 mu0=50 10 180;
   mcmc plots=(trace(mean(Oxygen)) acf(mean(Oxygen)));
   var Oxygen RunTime RunPulse;
run;

For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.

The global plot option LOG requests that the logarithmic transformations of parameters be used. The default is PLOTS=TRACE(MEAN).

The available trace-options are as follows:

MEAN < ( variables ) >: displays plots of means for continuous variables in the list. When the MEAN option is specified without variables, all continuous variables are used.
STD < ( variables ) >: displays plots of standard deviations for continuous variables in the list. When the STD option is specified without variables, all continuous variables are used.

The discriminant function, logistic regression, regression, and predictive mean matching methods are available in the FCS statement. You specify each method with the syntax

method < (<imputed < = effects > > </ options>) >

That is, for each method, you can specify the imputed variables and, optionally, a set of effects to impute these variables. Each effect is a variable or a combination of variables in the VAR statement. The syntax for the specification of effects is the same as for the GLM procedure. See Chapter 46: The GLM Procedure, for more information.

One general form of an effect involving several variables is

X1 * X2 * A * B * C ( D E )

where A, B, C, D, and E are classification variables and X1 and X2 are continuous variables.

When an FCS statement is used without specifying any methods, the regression method is used for all imputed continuous variables and the discriminant function method is used for all imputed classification variables. In this case, for each imputed continuous variable, all other variables in the VAR statement are used as the covariates, and for each imputed classification variable, all other continuous variables in the VAR statement are used as the covariates.

When a method for continuous variables is specified without imputed variables, the method is used for all continuous variables in the VAR statement that are not specified in other methods. Similarly, when a method for classification variables is specified without imputed variables, the method is used for all classification variables in the VAR statement that are not specified in other methods.

For each imputed variable that does not use the discriminant function method, if no covariates are specified, then all other variables in the VAR statement are used as the covariates. That is, each continuous variable is used as a regressor effect, and each classification variable is used as a main effect. For an imputed variable that uses the discriminant function method, if no covariates are specified, then all other variables in the VAR statement are used as the covariates with the CLASSEFFECTS=INCLUDE option, and all other continuous variables in the VAR statement are used as the covariates with the CLASSEFFECTS=EXCLUDE option (which is the default).

With an FCS statement, the variables are imputed sequentially in the order specified in the VAR statement. For a continuous variable, you can use a regression method or a regression predicted mean matching method to impute missing values. For a nominal classification variable, you can use either a discriminant function method or a logistic regression method (generalized logit model) to impute missing values without using the ordering of the class levels. For an ordinal classification variable, you can use a logistic regression method (cumulative logit model) to impute missing values by using the ordering of the class levels. For a binary classification variable, either a discriminant function method or a logistic regression method can be used. By default, a regression method is used for a continuous variable, and a discriminant function method is used for a classification variable.

Note that except for the regression method, all other methods impute values from the observed values. See the section FCS Methods for Data Sets with Arbitrary Missing Patterns for a detailed description of the FCS methods.

You can specify the following imputation methods in an FCS statement (in alphabetical order):

DISCRIM <( imputed < = effects> </ options> ) >

specifies the discriminant function method of classification variables. The available options are as follows:

CLASSEFFECTS=EXCLUDE | INCLUDE: specifies whether the CLASS variables are used as covariate effects. The CLASSEFFECTS=EXCLUDE option excludes the CLASS variables from covariate effects and the CLASSEFFECTS=INCLUDE option includes the CLASS variables as covariate effects. The default is CLASSEFFECTS=EXCLUDE.
DETAILS: displays the group means and pooled covariance matrix used in each imputation.
PCOV=FIXED | POSTERIOR: specifies the pooled covariance used in the discriminant method. The PCOV=FIXED option uses the observed-data pooled covariance matrix for each imputation and the PCOV=POSTERIOR option draws a pooled covariance matrix from its posterior distribution. The default is PCOV=POSTERIOR.
PRIOR=EQUAL | JEFFREYS <=c> | PROPORTIONAL | RIDGE <=d>: specifies the prior probabilities of group membership. The PRIOR=EQUAL option sets the prior probabilities equal for all groups; the PRIOR=JEFFREYS <=c> option specifies a noninformative prior, 0 < c < 1; the PRIOR=PROPORTIONAL option sets the prior probabilities proportion to the group sample sizes; and the PRIOR=RIDGE <=d> option specifies a ridge prior, d > 0. If the noninformative prior c is not specified, c=0.5 is used. If the ridge prior d is not specified, d=0.25 is used. The default is PRIOR=JEFFREYS.

See the section Monotone and FCS Discriminant Function Methods for a detailed description of the method.

LOGISTIC <( imputed < = effects> </ options> ) >

specifies the logistic regression method for classification variables. The available options are as follows:

DESCENDING

reverses the sort order for the levels of the response variables.

DETAILS

displays the regression coefficients in the logistic regression model used in each imputation.

LIKELIHOOD=NOAUGMENT LIKELIHOOD=AUGMENT <( WEIGHT=w | NPARM <(MULT=m)> )>

specifies whether to add new observations to the likelihood function in the computation of maximum likelihood estimates. The LIKELIHOOD=AUGMENT option adds observations in each response group to the likelihood function, and the LIKELIHOOD=NOAUGMENT option makes no adjustment to the likelihood function. By default, LIKELIHOOD=NOAUGMENT.

The LIKELIHOOD=AUGMENT option is useful when the maximum likelihood parameter estimates do not exist. When LIKELIHOOD=AUGMENT, each added observation contributes the same weight, and the WEIGHT= option specifies the total added weight:

WEIGHT=w: explicitly specifies the total added weight w.
WEIGHT=NPARM <(MULT=m)>: uses the number of parameters in the logistic regression model as the total added weight. For example, for a simple binary logistic regression model that consists only of p continuous effects, the added weight is p+1. The MULT=m option specifies the multiplier for the total added weight, 0 <m $\leq$ 1, and the resulting total added weight is m times the number of parameters in the model. By default, MULT=1.

BY default, WEIGHT=NPARM. You can specify either the MULT=m suboption in WEIGHT=NPARM or the WEIGHT=w option to use a different total added weight in the computation of maximum likelihood estimates. For example, if the ratio between the number of parameters and the number of available observations (before augmentation) is large, you can use either MULT=m or WEIGHT=w to reduce the weight for the added observations (that is, reduce the effect from the added observations in the computation of maximum likelihood estimates). For more information about the augmented data approach, see the section Logistic Regression with Augmented Data.

LINK=GLOGIT | LOGIT

specifies the link function that links the response probabilities to the linear predictors. The LINK=LOGIT option (which is the default) uses the log odds function to fit the binary logit model when there are two response categories and to fit the cumulative logit model when there are more than two response categories. The LINK=GLOGIT option uses the generalized logit function to fit the generalized logit model, in which each nonreference category is contrasted with the last category.

ORDER=DATA | FORMATTED | FREQ | INTERNAL

specifies the sort order for the levels of the response variable. The ORDER=DATA sorts by the order of appearance in the input data set; the ORDER=FORMATTED sorts by their external formatted values; the ORDER=FREQ sorts by the descending frequency counts; and the ORDER=INTERNAL sorts by the unformatted values. The default is ORDER=FORMATTED.

See the section Monotone and FCS Logistic Regression Methods for a detailed description of the method.

REG | REGRESSION <( imputed < = effects> </ DETAILS> ) >

specifies the regression method of continuous variables. The DETAILS option displays the regression coefficients in the regression model used in each imputation.

With a regression method, the MAXIMUM=, MINIMUM=, and ROUND= options can be used to make the imputed values more consistent with the observed variable values.

See the section Monotone and FCS Regression Methods for a detailed description of the method.

REGPMM < ( imputed < = effects> < / options> ) > REGPREDMEANMATCH < ( imputed < = effects > < / options > ) >

specifies the predictive mean matching method for continuous variables. This method is similar to the regression method except that it imputes a value randomly from a set of observed values whose predicted values are closest to the predicted value for the missing value from the simulated regression model (Heitjan and Little 1991; Schenker and Taylor 1996).

The available options are DETAILS and K=. The DETAILS option displays the regression coefficients in the regression model used in each imputation. The K= option specifies the number of closest observations to be used in the selection. The default is K=5.

See the section Monotone and FCS Predictive Mean Matching Methods for a detailed description of the method.

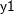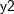With an FCS statement, the missing values of variables in the VAR statement are imputed. After the initial filled in, these variables with missing values are imputed sequentially in the order specified in the VAR statement in each iteration. 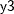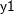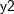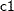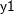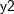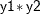For example, the following MI procedure statements use the regression method to impute variable $\Variable{y1}$ from effect $\Variable{y2}$ , the regression method to impute variable $\Variable{y3}$ from effects $\Variable{y1}$ and $\Variable{y2}$ , the logistic regression method to impute variable $\Variable{c1}$ from effects $\Variable{y1}$ , $\Variable{y2}$ , and $\Variable{y1}*\Variable{y2}$ , and the default regression method for continuous variables to impute variable 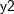$\Variable{y2}$ from effects 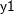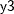$\Variable{y1}$ , $\Variable{y3}$ , and $\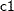Variable{c1}$ :

proc mi;
   class c1;
   fcs reg(y1= y2);
   fcs reg(y3= y1 y2);
   fcs logistic(c1= y1 y2 y1*y2);
   var y1 y2 y3 c1;
run;