The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples
 EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set
EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set - References
Imputer’s Model Versus Analyst’s Model
Multiple imputation inference assumes that the model you used to analyze the multiply imputed data (the analyst’s model) is the same as the model used to impute missing values in multiple imputation (the imputer’s model). But in practice, the two models might not be the same (Schafer 1997, p. 139).
Schafer (1997, pp. 139–143) provides comprehensive coverage of this topic, and the following example is based on his work.
Consider a trivariate data set with variables 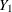 and
and 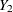 fully observed, and a variable
fully observed, and a variable 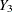 with missing values. An imputer creates multiple imputations with the model
with missing values. An imputer creates multiple imputations with the model 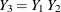 . However, the analyst can later use the simpler model
. However, the analyst can later use the simpler model 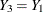 . In this case, the analyst assumes more than the imputer. That is, the analyst assumes there is no relationship between variables
. In this case, the analyst assumes more than the imputer. That is, the analyst assumes there is no relationship between variables
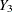 and
and 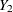 .
.
The effect of the discrepancy between the models depends on whether the analyst’s additional assumption is true. If the assumption
is true, the imputer’s model still applies. The inferences derived from multiple imputations will still be valid, although
they might be somewhat conservative because they reflect the additional uncertainty of estimating the relationship between
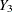 and
and 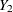 .
.
On the other hand, suppose that the analyst models 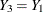 , and there is a relationship between variables
, and there is a relationship between variables 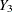 and
and 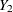 . Then the model
. Then the model 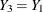 will be biased and is inappropriate. Appropriate results can be generated only from appropriate analyst models.
will be biased and is inappropriate. Appropriate results can be generated only from appropriate analyst models.
Another type of discrepancy occurs when the imputer assumes more than the analyst. For example, suppose that an imputer creates
multiple imputations with the model 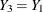 , but the analyst later fits a model
, but the analyst later fits a model 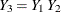 . When the assumption is true, the imputer’s model is a correct model and the inferences still hold.
. When the assumption is true, the imputer’s model is a correct model and the inferences still hold.
On the other hand, suppose there is a relationship between 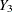 and
and 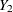 . Imputations created under the incorrect assumption that there is no relationship between
. Imputations created under the incorrect assumption that there is no relationship between 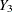 and
and 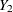 will make the analyst’s estimate of the relationship biased toward zero. Multiple imputations created under an incorrect
model can lead to incorrect conclusions.
will make the analyst’s estimate of the relationship biased toward zero. Multiple imputations created under an incorrect
model can lead to incorrect conclusions.
Thus, generally you should include as many variables as you can when doing multiple imputation. The precision you lose with included unimportant predictors is usually a relatively small price to pay for the general validity of analyses of the resultant multiply imputed data set (Rubin 1996). But at the same time, you need to keep the model building and fitting feasible (Barnard and Meng 1999, pp. 19–20).
To produce high-quality imputations for a particular variable, the imputation model should also include variables that are potentially related to the imputed variable and variables that are potentially related to the missingness of the imputed variable (Schafer 1997, p. 143).
Similar suggestions were also given by Van Buuren, Boshuizen, and Knook (1999, p. 687). They recommend that the imputation model include three sets of covariates: variables in the analyst’s model, variables associated with the missingness of the imputed variable, and variables correlated with the imputed variable. They also recommend the removal of the covariates not in the analyst’s model if they have too many missing values for observations with missing imputed variables.
Note that it is good practice to include a description of the imputer’s model with the multiply imputed data set (Rubin 1996, p. 479). That way, the analysts will have information about the variables involved in the imputation and which relationships among the variables have been implicitly set to zero.