The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples
 EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set
EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set - References
Example 75.18 Adjusting Imputed Values with Parameters in a Data Set
This example illustrates the pattern-mixture model approach in multiple imputation under the MNAR assumption by adjusting imputed values, using parameters that are stored in a data set.
Suppose that a pharmaceutical company is conducting a clinical trial to test the efficacy of a new drug. The trial consists
of two groups of equally allocated patients: a treatment group that receives the new drug and a placebo control group. The
variable Trt is an indicator variable, with a value of 1 for patients in the treatment group and a value of 0 for patients in the control
group. The variable Y0 is the baseline efficacy score, and the variable Y1 is the efficacy score at a follow-up visit.
If the data set does not contain any missing values, then a regression model such as
![\[ \Variable{Y1} \, =\, \Variable{Trt} \; \; \Variable{Y0} \]](images/statug_mi0390.png)
can be used to test the efficacy of the treatment effect.
Now suppose that the variables Trt and Y0 are fully observed and the variable Y1 contains missing values in both the treatment and control groups. Table 75.12 shows the variables in the data set.
Table 75.12: Variables
|
Variables |
||
|---|---|---|
|
Trt |
Y0 |
Y1 |
|
0 |
X |
X |
|
1 |
X |
X |
|
0 |
X |
. |
|
1 |
X |
. |
Suppose the data set Mono3 contains the data from the trial that have missing values in Y1. Output 75.18.1 lists the first 10 observations.
Output 75.18.1: Clinical Trial Data
Multiple imputation often assumes that missing values are MAR. Here, however, it is plausible that the distributions of missing
Y1 responses in the treatment and control groups have lower expected values than the corresponding distributions of the observed
Y1 responses. Carpenter and Kenward (2013, pp. 129–130) describe an implementation of the pattern-mixture model approach that uses different shift parameters for the
treatment and control groups, where the two parameters are correlated.
Assume that the expected shifts of the missing follow-up responses in the control and treatment groups, 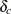 and
and 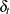 , have a multivariate normal distribution
, have a multivariate normal distribution
![\[ \left( \begin{array}{rrr} \delta _ c \\ \delta _ t \\ \end{array} \right) \; \sim \; N \left( \, \left( \begin{array}{rrr} -0.5 \\ -1 \\ \end{array} \right) \, , \left( \begin{array}{rrr} 0.01 & 0.001 \\ 0.001 & 0.01 \\ \end{array} \right) \right) \]](images/statug_mi0397.png)
The following statements generate shift parameters for the control and treatment groups for six imputations:
proc iml;
nimpute= 10;
call randseed( 15323);
mean= { -0.5 -1};
cov= { 0.01 0.001 , 0.001 0.01};
/*---- Simulate nimpute bivariate normal variates ----*/
d= randnormal( nimpute, mean, cov);
impu= j(nimpute, 1, 0);
do j=1 to nimpute; impu[j,]= j; end;
delta= impu || d;
/*--- Output shift parameters for groups ----*/
create parm1 from delta[colname={_Imputation_ Shift_C Shift_T}];
append from delta;
quit;
Output 75.18.2 lists the generated shift parameters in Parm1.
Output 75.18.2: Shift Parameters for Imputations
The following statements impute missing values for Y1 under the MNAR assumption. The shift parameters for the 10 imputations that are stored in the Parm1 data set are used to adjust the imputed values.
proc mi data=Mono3 seed=1423741 nimpute=10 out=outex18;
class Trt;
monotone reg;
mnar adjust( y1 / adjustobs=(Trt='0') parms(shift=shift_c)=parm1)
adjust( y1 / adjustobs=(Trt='1') parms(shift=shift_t)=parm1);
var Trt y0 y1;
run;
The ADJUST option specifies parameters for adjusting the imputed values of Y1 for specified subsets of observations. The first ADJUST option specifies that the shift parameters that are stored in the
variable SHIFT_C are to be applied to the imputed Y1 values of observations where TRT=0 for the corresponding imputations. The second ADJUST option specifies that the shift parameters
that are stored in the variable SHIFT_T are to be applied to the imputed Y1 values of observations where TRT=1 for the corresponding imputations.
The "Model Information" table in Output 75.18.3 describes the method that is used in the multiple imputation process.
Output 75.18.3: Model Information
The "Monotone Model Specification" table in Output 75.18.4 describes methods and imputed variables in the imputation model. The MI procedure uses the regression method to impute the
variable Y1.
Output 75.18.4: Monotone Model Specification
The "Missing Data Patterns" table in Output 75.18.5 lists distinct missing data patterns and their corresponding frequencies and percentages. The table confirms a monotone missing pattern for these variables.
Output 75.18.5: Missing Data Patterns
The "MNAR Adjustments to Imputed Values" table in Output 75.18.6 lists the adjustment parameters for the 10 imputations.
Output 75.18.6: MNAR Adjustments to Imputed Values
| MNAR Adjustments to Imputed Values |
|||
|---|---|---|---|
| Imputed Variable |
Imputation | Observations | Shift |
| y1 | 1 | Trt = 0 | -0.5699 |
| 1 | Trt = 1 | -0.9049 | |
| 2 | Trt = 0 | -0.3868 | |
| 2 | Trt = 1 | -0.8452 | |
| 3 | Trt = 0 | -0.5834 | |
| 3 | Trt = 1 | -0.9279 | |
| 4 | Trt = 0 | -0.4821 | |
| 4 | Trt = 1 | -0.9903 | |
| 5 | Trt = 0 | -0.5719 | |
| 5 | Trt = 1 | -1.0209 | |
| 6 | Trt = 0 | -0.5760 | |
| 6 | Trt = 1 | -1.0085 | |
| 7 | Trt = 0 | -0.4417 | |
| 7 | Trt = 1 | -0.9325 | |
| 8 | Trt = 0 | -0.5331 | |
| 8 | Trt = 1 | -1.0661 | |
| 9 | Trt = 0 | -0.5328 | |
| 9 | Trt = 1 | -1.1669 | |
| 10 | Trt = 0 | -0.5350 | |
| 10 | Trt = 1 | -1.1101 | |
The following statements list the first 10 observations of the data set Outex18 in Output 75.18.7:
proc print data=outex18(obs=10); var _Imputation_ Trt Y0 Y1; title 'First 10 Observations of the Imputed Data Set'; run;
Output 75.18.7: Imputed Data Set