The MI Procedure

Multiple Imputation Efficiency

The relative efficiency (RE) of using the finite m imputation estimator, rather than using an infinite number for the fully efficient imputation, in units of variance, is approximately a function of m and 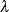${\lambda }$ (Rubin 1987, p. 114):

\[ \mr{RE} = { \left( 1 + \frac{\lambda }{m} \right) }^{-1} \]

where mis the number of imputations and 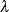${\lambda }$ is the fraction of missing information.

Table 75.7 shows relative efficiencies with different values of m and 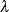${\lambda }$.

Table 75.7: Relative Efficiencies

   

$\blambda $

m

 

10%

20%

30%

50%

70%

3

 

0.9677

0.9375

0.9091

0.8571

0.8108

5

 

0.9804

0.9615

0.9434

0.9091

0.8772

10

 

0.9901

0.9804

0.9709

0.9524

0.9346

20

 

0.9950

0.9901

0.9852

0.9756

0.9662


The table shows that if the fraction of missing information is modest, only a small number of imputations are needed. For example, if 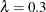${\lambda }=0.3$, only three imputations are needed to have a 91% efficiency and five imputations are needed to have a 94% efficiency.