The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples
 EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set
EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set - References
Sensitivity Analysis for the MAR Assumption
Multiple imputation usually assumes that the data are missing at random (MAR). Suppose the data set contains variables 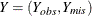 , where
, where 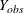 are fully observed variables and
are fully observed variables and 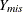 is a variable that contains missing observations. Also suppose
is a variable that contains missing observations. Also suppose  is a response indicator whose element is 0 or 1, depending on whether
is a response indicator whose element is 0 or 1, depending on whether 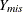 is missing or observed. Then the MAR assumption is that the probability that a
is missing or observed. Then the MAR assumption is that the probability that a 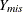 observation is missing can depend on
observation is missing can depend on 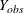 but not on
but not on 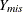 . That is,
. That is,
![\[ \mr{pr}(\, \mb{R} ~ |~ Y_{\mathit{obs}}, Y_{\mathit{mis}} \, ) = \mr{pr}(\, \mb{R} ~ |~ Y_{\mathit{obs}} \, ) \]](images/statug_mi0318.png)
The MAR assumption cannot be verified, because the missing values are not observed. In clinical trials, for a study that assumes MAR, the sensitivity of inferences to departures from the MAR assumption should be examined, as recommended by the National Research Council (2010, p. 111):
Recommendation 15: Sensitivity analysis should be part of the primary reporting of findings from clinical trials. Examining sensitivity to the assumptions about the missing data mechanism should be a mandatory component of reporting.
If it is plausible that the missing data are not MAR, you can perform sensitivity analysis under the missing not at random (MNAR) assumption. You can generate inferences for various scenarios under MNAR and then examine the results. If the results under MNAR differ from the results under MAR, then the conclusion under MAR is in question.
Based on the factorization of the joint distribution  , there are two common strategies for sensitivity analysis under MNAR: the pattern-mixture model approach and the selection
model approach. The pattern-mixture model approach is implemented in the MI procedure because it is natural and straightforward.
, there are two common strategies for sensitivity analysis under MNAR: the pattern-mixture model approach and the selection
model approach. The pattern-mixture model approach is implemented in the MI procedure because it is natural and straightforward.
Pattern-Mixture Model Approach
In the pattern-mixture model approach (Little 1993; Molenberghs and Kenward 2007, pp. 30, 34–37; National Research Council 2010, pp. 88–89), the joint distribution is factorized as
![\[ \mr{pr}(\, Y, \mb{R} \, ) = \mr{pr}(\, Y ~ |~ \mb{R} ) \; \mr{pr}(\, \mb{R} \, ) \]](images/statug_mi0320.png)
This allows for different distributions for missing values and for observed values. For example,
![\[ \mr{pr}(\, Y, \mb{R} \, ) = \mr{pr}(\, Y ~ |~ \mb{R} ) \; \mr{pr}( \mb{R} \, ) = \mr{pr}(\, Y ~ |~ \mb{R=1} ) \; \mr{pr}( \mb{R=1} \, ) + \mr{pr}(\, Y ~ |~ \mb{R=0} ) \; \mr{pr}( \mb{R=0} \, ) \]](images/statug_mi0321.png)
which is a mixture of distributions for two different patterns. Here, the "pattern" refers to a group of observations that have the same distribution; the term is not used in the same sense as "missing data pattern."
In the pattern-mixture model approach, the joint distribution is factored as
![\[ \mr{pr}( Y_{\mathit{obs}}, Y_{\mathit{mis}}, \mb{R} ) = \mr{pr}( Y_{\mathit{mis}} ~ |~ Y_{\mathit{obs}}, \mb{R} ) \; \mr{pr}( Y_{\mathit{obs}}, \mb{R} ) \]](images/statug_mi0322.png)
and under the MNAR assumption,
![\[ \mr{pr}(\, Y_{\mathit{mis}} ~ |~ Y_{\mathit{obs}}, \mb{R}=0 \, ) \neq \mr{pr}(\, Y_{\mathit{mis}} ~ |~ Y_{\mathit{obs}}, \mb{R}=1 \, ) \]](images/statug_mi0323.png)
It is straightforward to create imputations by using pattern-mixture models. The next three sections provide details for this approach.
Selection Model Approach
In the selection model approach (Rubin 1987, p. 207; Little and Rubin 2002, pp. 313–314; Molenberghs and Kenward 2007, p. 30), the joint distribution is factorized as
![\[ \mr{pr}( Y, \mb{R} ) = \mr{pr}( \mb{R} ~ |~ Y ) \; \, \mr{pr}( Y ) \]](images/statug_mi0324.png)
where  ,
,  is the marginal distribution of
is the marginal distribution of Y, and  is the conditional distribution of the missing mechanism R given
is the conditional distribution of the missing mechanism R given Y. The term "selection" comes from the specification of R that selects individuals to be observed in the conditional distribution
 . Both distributions,
. Both distributions,  and
and  , must be specified for the analysis. The MI procedure does not provide this approach.
, must be specified for the analysis. The MI procedure does not provide this approach.