The MI Procedure

Checking Convergence in MCMC

Subsections:

The theoretical convergence of the MCMC method has been explored under various conditions, as described in Schafer (1997, p. 70). However, in practice, verification of convergence is not a simple matter.

The parameters used in the imputation step for each iteration can be saved in an output data set with the OUTITER= option. These include the means, standard deviations, covariances, worst linear function, and observed-data LR statistics. You can then monitor the convergence in a single chain by displaying trace plots and autocorrelations for those parameter values (Schafer 1997, p. 120). The trace and autocorrelation function plots for parameters such as variable means, covariances, and the worst linear function can be displayed by specifying the PLOTS=TRACE and PLOTS=ACF options, respectively.

You can apply the EM algorithm to a bootstrap sample to obtain overdispersed starting values for multiple chains (Gelman and Rubin 1992). This provides a conservative estimate of the number of iterations needed before each imputation.

The next four subsections describe useful statistics and plots that can be used to check the convergence of the MCMC method.

LR Statistics

You can save the observed-data likelihood ratio (LR) statistic in each iteration with the LR option in the OUTITER= data set. The statistic is based on the observed-data likelihood with parameter values used in the iteration and the observed-data maximum likelihood derived from the EM algorithm.

In each iteration, the LR statistic is given by

\[ -2 \, \mr{log} \, \left( \frac{ f( \hat{\btheta }_{i}) }{ f( \hat{\btheta }) } \right) \]

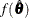where $f( \hat{\btheta })$ is the observed-data maximum likelihood derived from the EM algorithm and 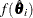$f( \hat{\btheta }_{i})$ is the observed-data likelihood for 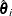$\hat{\btheta }_{i}$ used in the iteration.

Similarly, you can also save the observed-data LR posterior mode statistic for each iteration with the LR_POST option. This statistic is based on the observed-data posterior density with parameter values used in each iteration and the observed-data posterior mode derived from the EM algorithm for posterior mode.

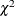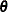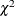For large samples, these LR statistics tends to be approximately ${\chi }^{2}$ distributed with degrees of freedom equal to the dimension of $\btheta $ (Schafer 1997, p. 131). For example, with a large number of iterations, if the values of the LR statistic do not behave like a random sample from the described ${\chi }^{2}$ distribution, then there is evidence that the MCMC method has not converged.

Worst Linear Function of Parameters

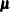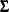The worst linear function (WLF) of parameters (Schafer 1997, pp. 129–131) is a scalar function of parameters $\bmu $ and $\bSigma $ that is "worst" in the sense that its function values converge most slowly among parameters in the MCMC method. The convergence of this function is evidence that other parameters are likely to converge as well.

For linear functions of parameters 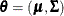$\btheta = ( \bmu , \bSigma )$, a worst linear function of 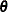$\btheta $ has the highest asymptotic rate of missing information. The function can be derived from the iterative values of 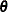$\btheta $ near the posterior mode in the EM algorithm. That is, an estimated worst linear function of 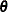$\btheta $ is

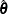\[ w( \btheta ) = \mb{v}’ \, ( \btheta - \hat{\btheta } ) \]

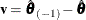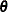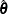where $\hat{\btheta }$ is the posterior mode and the coefficients $\mb{v}= \hat{\btheta }_{(-1)} - \hat{\btheta }$ are the difference between the estimated value of $\btheta $ one step prior to convergence and the converged value $\hat{\btheta }$.

You can display the coefficients of the worst linear function, $\mb{v}$, by specifying the WLF option in the MCMC statement. You can save the function value from each iteration in an OUTITER= data set by specifying the WLF option within the OUTITER option. You can also display the worst linear function values from iterations in an autocorrelation plot or a trace plot by specifying PLOTS=ACF(WLF) or PLOTS=TRACE(WLF), respectively.

Note that when the observed-data posterior is nearly normal, the WLF is one of the slowest functions to approach stationarity. When the posterior is not close to normal, other functions might take much longer than the WLF to converge, as described in Schafer (1997, p.130).

Trace Plot

A trace plot for a parameter 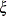${\xi }$ is a scatter plot of successive parameter estimates 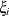${\xi }_ i$ against the iteration number i. The plot provides a simple way to examine the convergence behavior of the estimation algorithm for 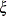${\xi }$. Long-term trends in the plot indicate that successive iterations are highly correlated and that the series of iterations has not converged.

You can display trace plots for worst linear function, variable means, variable variances, and covariances of variables. You can also request logarithmic transformations for positive parameters in the plots with the LOG option. When a parameter value is less than or equal to zero, the value is not displayed in the corresponding plot. See Example 75.11 for a usage of the trace plot.

Autocorrelation Function Plot

To examine relationships of successive parameter estimates 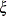${\xi }$, the autocorrelation function (ACF) can be used. For a stationary series, 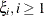${\xi }_ i, i \ge 1$, in trace data, the autocorrelation function at lag k is

\[ {\rho }_{k} = \frac{ \mr{Cov}({\xi }_ i, {\xi }_{i+k}) }{ \mr{Var}({\xi }_ i) } \]

The sample kth order autocorrelation is computed as

\[ r_{k} = \frac{\sum _{i=1}^{n-k} ({\xi }_ i-\overline{\xi }) ({\xi }_{i+k}-\overline{\xi }) }{\sum _{i=1}^ n ({\xi }_ i-\overline{\xi })^2} \]

You can display autocorrelation function plots for the worst linear function, variable means, variable variances, and covariances of variables. You can also request logarithmic transformations for parameters in the plots with the LOG option. When a parameter has values less than or equal to zero, the corresponding plot is not created.

You specify the maximum number of lags of the series with the NLAG= option. The autocorrelations at each lag less than or equal to the specified lag are displayed in the graph. In addition, the plot also displays approximate 95% confidence limits for the autocorrelations. At lag k, the confidence limits indicate a set of approximate 95% critical values for testing the hypothesis 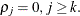${\rho }_{j}=0, j \ge k.$ See Example 75.11 for an illustration of the autocorrelation function plot.