The MI Procedure
- Overview
- Getting Started
-
Syntax
-
DetailsDescriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
-
ExamplesEM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set
- References
Number of Imputations
In multiple imputation, the number of imputations, m, must be specified in advance. The classic recommendation of a small m is based on a relative efficiency argument. For example, with 30% missing information, only three imputations are needed for 91% efficiency and five imputations are needed for 94% efficiency. Thus, often as few as three to five imputations are adequate in multiple imputation (Rubin 1996, p. 480). For more information about the relative efficiency of an estimator based on m imputations, see the section Multiple Imputation Efficiency.
Recent studies by Graham, Olchowski, and Gilreath (2007); Bodner (2008); and Von Hippel (2009, p. 278) note that a small number of imputations that suffice for high relative efficiency might not be adequate for other inferential goals, such as confidence intervals and p-values. These studies recommend much larger numbers of imputations.
Graham, Olchowski, and Gilreath (2007) use simulations to examine the effect of m on the power of a hypothesis test, and they recommend the use of many more imputations than the classic recommendation of three to five imputations. For example, with a 1% power falloff tolerance in multiple imputation, as compared to an infinite number of imputations, multiple imputation requires 20 imputations for 30% missing information and 40 imputations for 50% missing information (Graham, Olchowski, and Gilreath 2007, p. 212).
Bodner (2008) points out that with small m there is substantial imprecision in important statistics such as p-values and widths of confidence intervals. That is, different conclusions might be drawn for the same test in separate multiple
imputation runs. Bodner (2008) uses simulation to compute the minimum number of imputations that are needed for an estimated 95% confidence interval width
to achieve a specified precision. For example, for a 95% confidence interval width to be within 10% of its true value 95%
of the time, multiple imputation requires 24 imputations if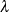 
= 0.3 and 59 imputations if 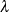= 0.5 (Bodner 2008, p. 668), where 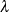is the fraction of missing information. Because 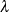is unknown, a conservative estimate of 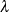is the proportion of cases with missing values (Bodner 2008, p. 670).
Von Hippel (2009, p. 278) shows that with a small number of imputations, only the point estimates are reliable. That is, the point estimates
will not change much if the missing values are imputed again. For other statistics (such as standard error and p-value) to be reliable, the rule of thumb is to use the percentages of cases with missing values as the number of imputations.
White, Royston, and Wood (2011, pp. 387–388) also suggest the use of this rule of thumb, at least when 
, and the resulting number of imputations often provides an adequate level to reproduce the results if the missing values
are imputed again.
These recent studies suggest the use of a much larger number of imputations than the classic recommendation of three to five imputations. Thus, the default number of imputations in PROC MI has been changed from NIMPUTE=5 to NIMPUTE=25 in SAS/STAT 14.1. Alternatively, you can specify NIMPUTE=PCTMISSING to use the percentage of cases with missing values as the number of imputations.
In practice, you can verify the needed number of imputations informally by replicating sets of m imputations and checking whether the estimates are stable between sets (Horton and Lipsitz 2001, p. 246).