The MI Procedure

Missing values are an issue in a substantial number of statistical analyses. Most SAS statistical procedures exclude observations with any missing variable values from the analysis. These observations are called incomplete cases. While using only complete cases is simple, you lose information that is in the incomplete cases. Excluding observations with missing values also ignores the possible systematic difference between the complete cases and incomplete cases, and the resulting inference might not be applicable to the population of all cases, especially with a smaller number of complete cases.

Some SAS procedures use all the available cases in an analysis—that is, cases with useful information. For example, the CORR procedure estimates a variable mean by using all cases with nonmissing values for this variable, ignoring the possible missing values in other variables. The CORR procedure also estimates a correlation by using all cases with nonmissing values for this pair of variables. This estimation might make better use of the available data, but the resulting correlation matrix might not be positive definite.

Another strategy is single imputation, in which you substitute a value for each missing value. Standard statistical procedures for complete data analysis can then be used with the filled-in data set. For example, each missing value can be imputed from the variable mean of the complete cases. This approach treats missing values as if they were known in the complete-data analyses. Single imputation does not reflect the uncertainty about the predictions of the unknown missing values, and the resulting estimated variances of the parameter estimates are biased toward zero (Rubin 1987, p. 13).

Instead of filling in a single value for each missing value, multiple imputation replaces each missing value with a set of plausible values that represent the uncertainty about the right value to impute (Rubin 1976, 1987). The multiply imputed data sets are then analyzed by using standard procedures for complete data and combining the results from these analyses. No matter which complete-data analysis is used, the process of combining results from different data sets is essentially the same.

Multiple imputation does not attempt to estimate each missing value through simulated values, but rather to represent a random sample of the missing values. This process results in valid statistical inferences that properly reflect the uncertainty due to missing values; for example, valid confidence intervals for parameters.

Multiple imputation inference involves three distinct phases:

The MI procedure is a multiple imputation procedure that creates multiply imputed data sets for incomplete p-dimensional multivariate data. It uses methods that incorporate appropriate variability across the m imputations. The imputation method of choice depends on the patterns of missingness in the data and the type of the imputed variable.

A data set with variables 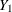, , 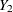…, 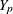(in that order) is said to have a monotone missing pattern when the event that a variable 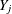is missing for a particular individual implies that all subsequent variables 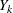, , 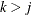are missing for that individual.

For data sets with monotone missing patterns, the variables with missing values can be imputed sequentially with covariates constructed from their corresponding sets of preceding variables. To impute missing values for a continuous variable, you can use a regression method (Rubin 1987, pp. 166–167), a predictive mean matching method (Heitjan and Little 1991; Schenker and Taylor 1996), or a propensity score method (Rubin 1987, pp. 124, 158; Lavori, Dawson, and Shera 1995). To impute missing values for a classification variable, you can use a logistic regression method when the classification variable has a binary, nominal, or ordinal response, or you can use a discriminant function method when the classification variable has a binary or nominal response.

For data sets with arbitrary missing patterns, you can use either of the following methods to impute missing values: a Markov chain Monte Carlo (MCMC) method (Schafer 1997) that assumes multivariate normality, or a fully conditional specification (FCS) method (Brand 1999; Van Buuren 2007) that assumes the existence of a joint distribution for all variables.

You can use the MCMC method to impute either all the missing values or just enough missing values to make the imputed data sets have monotone missing patterns. With a monotone missing data pattern, you have greater flexibility in your choice of imputation models, such as the monotone regression method that do not use Markov chains. You can also specify a different set of covariates for each imputed variable.

An FCS method does not start with an explicitly specified multivariate distribution for all variables, but rather uses a separate conditional distribution for each imputed variable. For each imputation, the process contains two phases: the preliminary filled-in phase followed by the imputation phase. At the filled-in phase, the missing values for all variables are filled in sequentially over the variables taken one at a time. These filled-in values provide starting values for these missing values at the imputation phase. At the imputation phase, the missing values for each variable are imputed sequentially for a number of burn-in iterations before the imputation.

As in methods for data sets with monotone missing patterns, you can use a regression method or a predictive mean matching method to impute missing values for a continuous variable, a logistic regression method to impute missing values for a classification variable with a binary or ordinal response, and a discriminant function method to impute missing values for a classification variable with a binary or nominal response.

After the m complete data sets are analyzed using standard SAS procedures, you can use the MIANALYZE procedure to generate valid statistical inferences about these parameters by combining results from the m analyses.

The number of imputations, m, must be specified in advance. The relative efficiency of an estimator based on a small number of imputations is high for cases with modest missing information (Rubin 1987, p. 114), and often a value of m as low as three or five is adequate (Rubin 1996, p. 480). For more information about relative efficiency, see the section Multiple Imputation Efficiency.

Although a small number of imputations can suffice for high relative efficiency, they might not be adequate for other aspects of inference, such as confidence intervals and p-values. Recent studies examine these aspects and recommend much larger values of m than the traditionally advised values of three to five (Allison 2012; Van Buuren 2012, pp. 49–50). For more information, see the section Number of Imputations.

Multiple imputation inference assumes that the model (variables) you used to analyze the multiply imputed data (the analyst’s model) is the same as the model used to impute missing values in multiple imputation (the imputer’s model). But in practice, the two models might not be the same. The consequences for different scenarios (Schafer 1997, pp. 139–143) are discussed in the section Imputer’s Model Versus Analyst’s Model.

Multiple imputation usually assumes that the data are missing at random (MAR). That is, for a variable Y, the probability that an observation is missing depends only on the observed values of other variables, not on the unobserved values of Y. The MAR assumption cannot be verified, because the missing values are not observed. For a study that assumes MAR, the sensitivity of inferences to departures from the MAR assumption should be examined.

The pattern-mixture model approach to sensitivity analysis models the distribution of a response as the mixture of a distribution of the observed responses and a distribution of the missing responses. Missing values can then be imputed under a plausible scenario for which the missing data are missing not at random (MNAR). If this scenario leads to a conclusion different from inference under MAR, then the MAR assumption is questionable.