The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyNumber of ImputationsImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples
 EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set
EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Methods for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set - References
Descriptive Statistics
Suppose 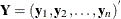 is the
is the 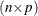 matrix of complete data, which might not be fully observed,
matrix of complete data, which might not be fully observed, 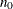 is the number of observations fully observed, and
is the number of observations fully observed, and 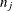 is the number of observations with observed values for variable
is the number of observations with observed values for variable 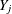 .
.
With complete cases, the sample mean vector is
![\[ \overline{\mb{y}} = \frac{1}{n_{0}} \sum {\mb{y}_{i}} \]](images/statug_mi0060.png)
and the CSSCP matrix is
![\[ \sum { ( \mb{y}_{i} - \overline{\mb{y}} ) ( \mb{y}_{i} - \overline{\mb{y}} )^{'} } \]](images/statug_mi0061.png)
where each summation is over the fully observed observations.
The sample covariance matrix is
![\[ \mb{S} = \frac{1}{\, n_{0}-1 \, } \sum { ( \mb{y}_{i} - \overline{\mb{y}} ) ( \mb{y}_{i} - \overline{\mb{y}} )^{'} } \]](images/statug_mi0062.png)
and is an unbiased estimate of the covariance matrix.
The correlation matrix 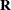 , which contains the Pearson product-moment correlations of the variables, is derived by scaling the corresponding covariance
matrix:
, which contains the Pearson product-moment correlations of the variables, is derived by scaling the corresponding covariance
matrix:
![\[ \mb{R} = \mb{D}^{-1} \mb{S} \, \mb{D}^{-1} \]](images/statug_mi0064.png)
where 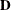 is a diagonal matrix whose diagonal elements are the square roots of the diagonal elements of
is a diagonal matrix whose diagonal elements are the square roots of the diagonal elements of 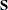 .
.
With available cases, the corrected sum of squares for variable 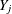 is
is
![\[ \sum { ( y_{ji} - {\overline y_{j}} )^2 } \]](images/statug_mi0066.png)
where 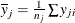 is the sample mean and each summation is over observations with observed values for variable
is the sample mean and each summation is over observations with observed values for variable 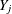 .
.
The variance is
![\[ s_{jj}^2 = \frac{1}{\, n_{j}-1 \, } \sum { ( y_{ji} - {\overline y_{j}} )^2 } \]](images/statug_mi0068.png)
The correlations for available cases contain pairwise correlations for each pair of variables. Each correlation is computed from all observations that have nonmissing values for the corresponding pair of variables.