The SEQDESIGN Procedure

Group Sequential Methods

Subsections:

For a group sequential design, there are two possible boundaries for a one-sided test and four possible boundaries for a two-sided test. Each boundary consists of one boundary value (critical value) for each stage. The SEQDESIGN procedure provides various methods for computing the boundary values.

The boundary value for a fixed-sample test cannot be applied to each stage of sequential design because, as shown by Armitage, McPherson, and Rowe (1969), repeated significance tests at a fixed level on accumulating data increase the probability of a Type I error. For example, with a fixed-sample two-sided test, the critical values 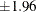$\pm 1.96$ for a standardized Z statistic produce a Type I error probability level 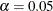$\alpha =0.05$. But for a two-sided group sequential test with two equally spaced stages, if the same critical values 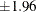$\pm 1.96$ are used to reject the null hypothesis at these two stages, the Type I error probability level is 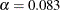$\alpha =0.083$, larger than the fixed-sample $\alpha $.

Numerous methods are available for deriving the critical values for each boundary in a sequential design. Pocock (1977) applies repeated significance tests to group sequential trials with equal-size groups and derives a constant critical value on the standardized normal Z scale across all stages that maintains the specified Type I error probability level. O’Brien and Fleming (1979) propose a sequential procedure that has boundary values (in absolute value) decrease over the stages on the standardized normal Z scale.

The SEQDESIGN procedure provides the following three types of methods:

  • fixed boundary shape methods, which derive boundaries with specified boundary shapes

  • Whitehead methods, which adjust boundaries derived for continuous monitoring so that they apply to discrete monitoring

  • error spending methods

Each type of methods uses a distinct approach to derive the boundary values for a group sequential trial. Whitehead methods require much less computation with resulting Type I error probability and power that are close but differ slightly from the specified values due to the approximations used in deriving the tests (Jennison and Turnbull 2000, p. 106). Fixed boundary shape methods derive boundary values by estimating a fixed number of parameters and require more computation. Error spending methods derive boundary values at each stage sequentially and require much more computation than other types of methods for group sequential trials with a large number of stages.

Within each type of methods, you can choose methods that creating boundary values range from conservative stopping boundary values at early stages to liberal stopping boundary values at very early stages.

You can use the SEQDESIGN procedure to specify methods from the same type for each design. A different method can be specified for each boundary separately, but all methods in a design must be of the same type.

Fixed Boundary Shape Methods

The fixed boundary shape methods include the unified family methods and the Haybittle-Peto method. The unified family methods (Kittelson and Emerson 1999) derive boundaries from specified boundary shapes. These methods include Pocock’s method (Pocock 1977) and the O’Brien-Fleming method (O’Brien and Fleming 1979) as special cases.

The Haybittle-Peto method (Haybittle 1971; Peto et al. 1976) uses a value of 3 for the critical values in interim stages, so the critical value at the final stage is close to the critical value for the fixed-sample design. In the SEQDESIGN procedure, the Haybittle-Peto method has been generalized to allow for different boundary values at interim stages.

Whitehead Methods

Whitehead and Stratton (1983) and Whitehead (1997, 2001) develop triangular and straight-line boundaries by adapting tests constructed for continuous monitoring to discrete monitoring of group sequential tests. With continuous monitoring, the values for each boundary fall in a straight line when plotted on the score statistic scale. The discrete boundary is derived by subtracting the expected overshoot from the continuous boundary to obtain the desired Type I and Type II error probabilities. For a design with early stopping to either reject or accept the null hypothesis, the boundaries form a triangle when plotted on the score statistic scale. See the section Score Statistic for a detailed description of the score statistic.

Error Spending Methods

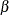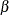For every sequential design, the $\alpha $ and $\beta $ errors at each stage can be computed from the boundary values. On the other hand, you can derive the boundary values from specified $\alpha $ and $\beta $ errors for each stage. The error spending function approach (Lan and DeMets 1983) uses an error spending function to specify the errors at each stage for each boundary and then derives the boundary values.