The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
Acceptance (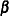 ) Boundary
) Boundary
In a group sequential trial, the rejection boundary is derived under the null hypothesis 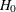 and is used to stop the trial early to reject
and is used to stop the trial early to reject 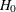 . Similarly, the acceptance boundary is derived under the alternative hypothesis and is used to stop the trial early to accept
. Similarly, the acceptance boundary is derived under the alternative hypothesis and is used to stop the trial early to accept
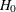 . But, for a trial with early stopping either to reject or to accept the null hypothesis, dependency exists between these
two boundaries. This section describes the effects of the acceptance boundary on the derivation of the rejection boundary
in a group sequential trial.
. But, for a trial with early stopping either to reject or to accept the null hypothesis, dependency exists between these
two boundaries. This section describes the effects of the acceptance boundary on the derivation of the rejection boundary
in a group sequential trial.
The following statements create a one-sided four-stage group sequential design with early stopping either to reject or to
accept 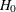 :
:
ods graphics on;
proc seqdesign altref=10;
ErrSpendPower_2: design nstages=4
method=errfuncpow(rho=2)
alt=upper stop=both
alpha=0.025 beta=0.10;
run;
The ALTREF=10 option specifies the alternative reference 10. The METHOD=ERRFUNCPOW(RHO=2) option uses a 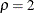 power family error spending method to generate the rejection boundary. The ALPHA=0.025 and BETA=0.10 options specify the
Type I error level 0.025 and Type II error level 0.10, respectively.
power family error spending method to generate the rejection boundary. The ALPHA=0.025 and BETA=0.10 options specify the
Type I error level 0.025 and Type II error level 0.10, respectively.
The power parameter 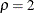 used in the design lies between
used in the design lies between 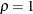 and
and 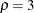 , where the boundaries created with the
, where the boundaries created with the 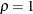 power family error spending method are similar to the boundaries created from the Pocock method, and the boundaries created
with
power family error spending method are similar to the boundaries created from the Pocock method, and the boundaries created
with 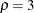 are similar to the boundaries created from the O’Brien-Fleming method.
are similar to the boundaries created from the O’Brien-Fleming method.
The "Boundary Information" table in Figure 101.12 shows the rejection and acceptance boundary values at the stages. With an error spending function method, the boundary values are derived sequentially. In particular, the rejection boundary value at a stage is derived conditionally on both rejection and acceptance boundary values at the previous stage. See the section Error Spending Methods for a detailed description of the error spending methods.
Figure 101.12: Boundary Information
| Boundary Information (Standardized Z Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | Upper | Beta | Alpha | |
| 1 | 0.2500 | 0.028605 | 1.69130 | -0.80640 | 2.95517 |
| 2 | 0.5000 | 0.05721 | 2.39186 | 0.37356 | 2.55934 |
| 3 | 0.7500 | 0.085815 | 2.92942 | 1.24940 | 2.29904 |
| 4 | 1.0000 | 0.11442 | 3.38261 | 2.04182 | 2.04182 |
With ODS Graphics enabled, the "Boundary Plot" is displayed by default, as shown in Figure 101.13. The continuation region is affected by the acceptance boundary, and the rejection boundary is thus adjusted for this acceptance boundary to maintain the Type I error level.
Figure 101.13: Boundary Plot
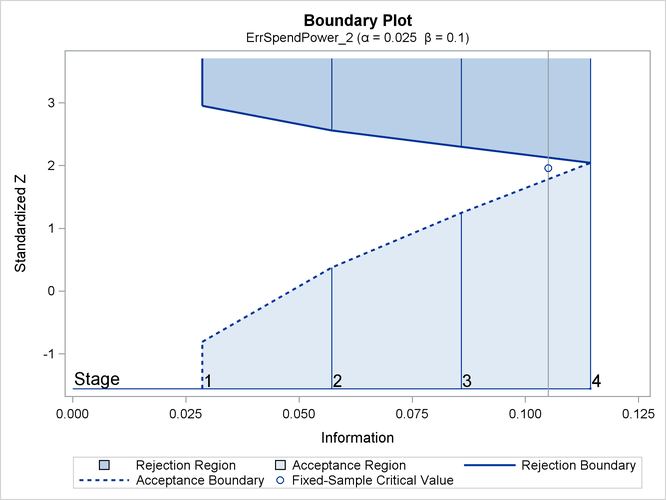
For a design with early stopping either to accept or to reject 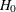 , the shapes of boundaries affect the critical value at the final stage. For the acceptance boundary, a liberal method at
early stages, such as a
, the shapes of boundaries affect the critical value at the final stage. For the acceptance boundary, a liberal method at
early stages, such as a 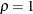 power family error spending method, lowers the critical value at the final stage. For the rejection boundary, a conservative
method at early stages, such as a
power family error spending method, lowers the critical value at the final stage. For the rejection boundary, a conservative
method at early stages, such as a 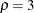 power family error spending method, also lowers the critical value at the final stage. In addition, a larger Type II error
level also lowers the critical value at the final stage. The resulting critical value at the final stage might even be less
than the critical value for the corresponding fixed-sample design.
power family error spending method, also lowers the critical value at the final stage. In addition, a larger Type II error
level also lowers the critical value at the final stage. The resulting critical value at the final stage might even be less
than the critical value for the corresponding fixed-sample design.
To illustrates how this can occur, the following statements use a 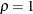 power family error spending method for the acceptance boundary and a
power family error spending method for the acceptance boundary and a 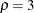 power family error spending method for the rejection boundary to create a group sequential design:
power family error spending method for the rejection boundary to create a group sequential design:
proc seqdesign altref=10;
ErrSpendPower_3_1: design nstages=4
method(alpha)=errfuncpow(rho=3)
method(beta)= errfuncpow(rho=1)
alt=upper stop=both
alpha=0.025 beta=0.10;
run;
The resulting "Boundary Information" table in Figure 101.14 shows that the boundary value at the final stage 1.9267 is less than 1.96, the critical value of the corresponding fixed-sample design.
Figure 101.14: Boundary Information
| Boundary Information (Standardized Z Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | Upper | Beta | Alpha | |
| 1 | 0.2500 | 0.029725 | 1.72410 | -0.23587 | 3.35935 |
| 2 | 0.5000 | 0.05945 | 2.43824 | 0.63117 | 2.76024 |
| 3 | 0.7500 | 0.089175 | 2.98622 | 1.31554 | 2.35119 |
| 4 | 1.0000 | 0.1189 | 3.44819 | 1.92672 | 1.92672 |
That is, 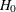 can be rejected even if the test statistic at the final stage is less than the critical value for the corresponding fixed-sample
design, which is not desirable. Therefore, for a design with an acceptance boundary, the design should be used with care.
can be rejected even if the test statistic at the final stage is less than the critical value for the corresponding fixed-sample
design, which is not desirable. Therefore, for a design with an acceptance boundary, the design should be used with care.
Another reason why the rejection boundary should not be affected by the acceptance boundary is that a Data and Safety Monitoring Board (DSMB) might not strictly adhere to this acceptance boundary, and thus the Type I error level might not be maintained. Therefore, it might not be desirable for the rejection boundary to be affected by the acceptance boundary (Lan and DeMets 2009, p. 103).
To use a design whose rejection boundary is not affected by the acceptance boundary and that can still stop the trial early
to accept 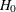 , you can use one of the following strategies:
, you can use one of the following strategies:
-
You can use the conditional power approach for a design that stops early only to reject
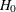 . For this design, the conditional power at an interim stage k can be defined as the total probability of rejecting
. For this design, the conditional power at an interim stage k can be defined as the total probability of rejecting 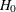 at any future stages under a specified hypothetical reference, given the observed statistic at stage k. A small conditional power indicates a small probability of success (rejecting
at any future stages under a specified hypothetical reference, given the observed statistic at stage k. A small conditional power indicates a small probability of success (rejecting 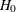 ) given the current data, and the trial can be stopped early to accept
) given the current data, and the trial can be stopped early to accept 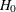 (Lan, Simon, and Halperin 1982; Lan and DeMets 2009, p. 101). For a detailed description of conditional power, see the section "Stochastic Curtailment" in Chapter 102: The SEQTEST Procedure.
(Lan, Simon, and Halperin 1982; Lan and DeMets 2009, p. 101). For a detailed description of conditional power, see the section "Stochastic Curtailment" in Chapter 102: The SEQTEST Procedure.
-
You can use a design with a nonbinding acceptance boundary (Zhu, Ni, and Yao 2011, pp. 132–133). For this design, the rejection boundary is created by ignoring the acceptance boundary. Thus, the Type I error level is maintained even when a trial is allowed to continue for a test statistic that falls in the acceptance region, and the rejection boundary values (with the standardized Z statistic scale) are identical to the boundary values that are derived in the corresponding design that stops early only to reject
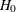 .
.