The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
Two-Sided Fixed-Sample Tests in Clinical Trials
A two-sided test is a test of a hypothesis with a two-sided alternative. Two-sided tests include simple symmetric tests and more complicated asymmetric tests that might have distinct lower and upper alternative references.
Symmetric Two-Sided Tests for Equality
For a symmetric two-sided test
with the null hypothesis 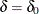 against the alternative
against the alternative 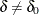 , an equivalent null hypothesis is
, an equivalent null hypothesis is 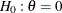 with a two-sided alternative
with a two-sided alternative 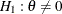 , where
, where 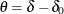 . A fixed-sample test rejects
. A fixed-sample test rejects 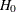 if
if 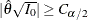 , where
, where 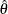 is a sample estimate of
is a sample estimate of 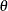 and
and 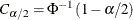 is the critical value.
is the critical value.
A common two-sided test is the test for the response difference between a treatment group and a control group. The null and
alternative hypotheses are 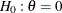 and
and 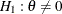 , respectively, where
, respectively, where 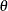 is the response difference between the two groups. If a greater value indicates a beneficial effect, then there are three
possible results:
is the response difference between the two groups. If a greater value indicates a beneficial effect, then there are three
possible results:
-
The test rejects the hypothesis
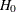 of equality and indicates that the treatment is significantly better if the standardized statistic
of equality and indicates that the treatment is significantly better if the standardized statistic 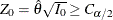 .
.
-
The test rejects the hypothesis
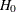 and indicates the treatment is significantly worse if the standardized statistic
and indicates the treatment is significantly worse if the standardized statistic 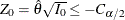 .
.
-
The test indicates no significant difference between the two responses if
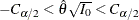 .
.
The p-value of the test is 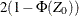 if
if 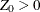 and
and 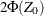 if
if 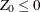 . The hypothesis
. The hypothesis 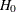 is rejected if the p-value of the test is less than
is rejected if the p-value of the test is less than  —that is, if
—that is, if 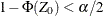 or
or 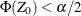 . A symmetric
. A symmetric 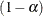 confidence interval for
confidence interval for 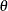 has lower and upper limits
has lower and upper limits
![\[ \left( \hat{\theta } - \frac{C_{\alpha /2}}{\sqrt {I_{0}}} \, , \, \, \, \hat{\theta } + \frac{C_{\alpha /2}}{\sqrt {I_{0}}} \right) \]](images/statug_seqdesign0286.png)
which is
![\[ \left( \frac{1}{ \sqrt {I_{0}} } \left( Z_{0} - C_{\alpha /2} \right) \, , \, \, \, \frac{1}{ \sqrt {I_{0}} } \left( Z_{0} + C_{\alpha /2} \right) \right) \]](images/statug_seqdesign0287.png)
The hypothesis 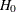 is rejected if the confidence interval for the parameter
is rejected if the confidence interval for the parameter 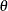 does not contain zero. That is, the lower limit is greater than zero or the upper limit is less than zero.
does not contain zero. That is, the lower limit is greater than zero or the upper limit is less than zero.
With an alternative reference 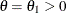 , a Type II error probability is defined as
, a Type II error probability is defined as
![\[ \beta = P_{\theta =\theta _1} ( - C_{\alpha /2} \, \, < \, \, Z_{0} \, \, < \, \, C_{\alpha /2} ) \]](images/statug_seqdesign0289.png)
which is
![\[ \beta = P_{\theta =\theta _1} \left( (-C_{\alpha /2} - \theta _1 \sqrt {I_{0}}) \, \, < \, \, (Z_{0} - \theta _1 \sqrt {I_{0}}) \, \, < \, \, (C_{\alpha /2} - \theta _1 \sqrt {I_{0}}) \right) \]](images/statug_seqdesign0290.png)
Thus
![\[ \beta = \Phi \left( C_{\alpha /2} - {\theta }_{1} \sqrt {I_{0}} \right) - \Phi \left( -C_{\alpha /2} - {\theta }_{1} \sqrt {I_{0}} \right) \]](images/statug_seqdesign0291.png)
The resulting power 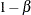 is the probability of correctly rejecting the null hypothesis, which includes the probability for the lower alternative and
the probability for the upper alternative. The SEQDESIGN procedure uses only the probability of correctly rejecting the null
hypothesis for the correct alternative in the power computation.
is the probability of correctly rejecting the null hypothesis, which includes the probability for the lower alternative and
the probability for the upper alternative. The SEQDESIGN procedure uses only the probability of correctly rejecting the null
hypothesis for the correct alternative in the power computation.
Thus, under the upper alternative hypothesis, the power in the SEQDESIGN procedure is computed as the probability of rejecting
the null hypothesis for the upper alternative, 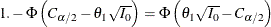 , and a very small probability of rejecting the null hypothesis for the lower alternative,
, and a very small probability of rejecting the null hypothesis for the lower alternative, 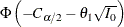 , is ignored. This power computation is more rational than the power based on the probability of correctly rejecting the null
hypothesis (Whitehead 1997, p. 75).
, is ignored. This power computation is more rational than the power based on the probability of correctly rejecting the null
hypothesis (Whitehead 1997, p. 75).
That is,
![\[ \beta = P_{\theta =\theta _1} \left( (Z_{0} - \theta _1 \sqrt {I_{0}}) \, \, < \, \, (C_{\alpha /2} - \theta _1 \sqrt {I_{0}}) \right) = \Phi \left( C_{\alpha /2} - \theta _1 \sqrt {I_{0}} \right) \]](images/statug_seqdesign0294.png)
Then with 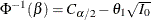 ,
,
![\[ \theta _1 \sqrt {I_{0}} = C_{\alpha /2} - {\Phi }^{-1}(\beta ) = {\Phi }^{-1}(1-\alpha /2) + {\Phi }^{-1}(1-\beta ) \]](images/statug_seqdesign0296.png)
The drift parameter 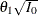 can be derived for specified
can be derived for specified  and
and 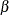 , and the maximum information is given by
, and the maximum information is given by
![\[ I_{0} = \, \left( \frac{ {\Phi }^{-1}(1-\alpha /2) + {\Phi }^{-1}(1-\beta ) }{ \theta _1 } \right)^{2} \]](images/statug_seqdesign0297.png)
If the maximum information is available, then the required sample size can be derived. For example, in a one-sample test for
mean, if the standard deviation  is known, the sample size n required for the test is
is known, the sample size n required for the test is
![\[ n= {\sigma }^{2} \, I_{0} = \, {\sigma }^{2} \left( \frac{{\Phi }^{-1}(1-\alpha /2) + {\Phi }^{-1}(1-\beta )}{\theta _1} \right)^{2} \]](images/statug_seqdesign0298.png)
On the other hand, if the alternative reference 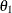 , standard deviation
, standard deviation  , and sample size n are all known, then
, and sample size n are all known, then  can be derived with a given
can be derived with a given 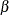 and, similarly,
and, similarly, 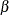 can be derived with a given
can be derived with a given  .
.
Generalized Two-Sided Tests for Equality
For a generalized two-sided test
with the null hypothesis 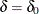 against the alternative
against the alternative 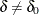 , an equivalent null hypothesis is
, an equivalent null hypothesis is 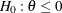 with a two-sided alternative
with a two-sided alternative 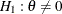 , where
, where 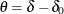 . A fixed-sample test rejects
. A fixed-sample test rejects 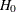 if the standardized statistic
if the standardized statistic 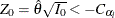 or
or 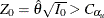 , where the critical values
, where the critical values 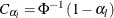 and
and 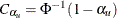 .
.
With the lower alternative reference 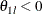 , a lower Type II error probability is defined as
, a lower Type II error probability is defined as
![\[ \beta _{l} = P_{\theta =\theta _{1l}} \left( -C_{\alpha _{l}} \, \leq \, Z_{0l} \sqrt {I_{0}} \right) = P_{\theta =\theta _{1l}} \left( -C_{\alpha _{l}} - \theta _{1l} \sqrt {I_{0}}\, \leq \, Z_{0l} \sqrt {I_{0}} - \theta _{1l} \sqrt {I_{0}} \right) \]](images/statug_seqdesign0304.png)
This implies
![\[ \beta _{l} = 1 - {\Phi }( -C_{\alpha _{l}} - \theta _{1l} \sqrt {I_{0}} ) \]](images/statug_seqdesign0305.png)
and the power is the probability of correctly rejecting the null hypothesis for the lower alternative,
![\[ 1 - \beta _{l} = {\Phi }( -C_{\alpha _{l}} - \theta _{1l} \sqrt {I_{0}} ) \]](images/statug_seqdesign0306.png)
The lower drift parameter is derived as
![\[ \theta _{1l} \sqrt {I_{0}} = - \left( \, {\Phi }^{-1}(1-\alpha _{l}) + {\Phi }^{-1}(1-\beta _{l}) \, \right) \]](images/statug_seqdesign0307.png)
Then, with specified 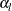 and
and 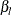 , if the maximum information is known, the lower alternative reference
, if the maximum information is known, the lower alternative reference 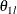 can be derived. If the maximum information is unknown, then with the specified lower alternative reference
can be derived. If the maximum information is unknown, then with the specified lower alternative reference 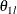 , the maximum information required is
, the maximum information required is
![\[ I_{0l} = \, \left( \frac{{\Phi }^{-1}(1-\alpha _{l}) + {\Phi }^{-1}(1-\beta _{l})}{-\theta _{1l}} \right)^{2} \]](images/statug_seqdesign0308.png)
Similarly, the upper drift parameter is derived as
![\[ \theta _{1u} \sqrt {I_{0}} = {\Phi }^{-1}(1-\alpha _{u}) + {\Phi }^{-1}(1-\beta _{u}) \]](images/statug_seqdesign0309.png)
For a given 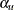 ,
, 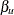 , and the upper alternative reference
, and the upper alternative reference 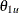 , the maximum information required is
, the maximum information required is
![\[ I_{0u} = \, \left( \frac{ {\Phi }^{-1}(1-\alpha _{u}) + {\Phi }^{-1}(1-\beta _{u}) }{ \theta _{1u} } \right)^{2} \]](images/statug_seqdesign0310.png)
Thus, the maximum information required for the design is given by
![\[ I_{0} = \mr{max} \, ( \, I_{0l}, \, I_{0u} ) \]](images/statug_seqdesign0311.png)
Note that with the maximum information level 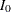 , if
, if 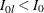 , then the derived power from the lower alternative is larger than the specified
, then the derived power from the lower alternative is larger than the specified 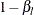 . Similarly, if
. Similarly, if 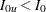 , then the derived power from the upper alternative is larger than the specified
, then the derived power from the upper alternative is larger than the specified 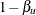 .
.
If maximum information is available, the required sample size can be derived. For example, in a one-sample test for mean,
if the standard deviation  is known, the sample size n required for the test is
is known, the sample size n required for the test is 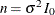 .
.
On the other hand, if the alternative references, Type I error probabilities 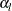 and
and 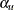 , standard deviation
, standard deviation  , and sample size n are all specified, then the Type II error probabilities
, and sample size n are all specified, then the Type II error probabilities 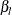 and
and 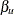 and the corresponding powers can be derived.
and the corresponding powers can be derived.