The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
Example 101.12 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept 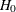
This example requests a four-stage two-sided asymmetric group sequential design for normally distributed statistics. The O’Brien-Fleming
boundary can be approximated by a gamma family error spending function with parameter 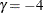 or –5, and the Pocock boundary can be approximated with parameter
or –5, and the Pocock boundary can be approximated with parameter 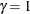 (Hwang, Shih, and DeCani 1990, p. 1440). The following statements use the gamma error spending function with early stopping to reject or accept the null
hypothesis
(Hwang, Shih, and DeCani 1990, p. 1440). The following statements use the gamma error spending function with early stopping to reject or accept the null
hypothesis 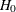 :
:
ods graphics on;
proc seqdesign altref=2
pss(cref=0 0.5 1)
stopprob(cref=0 1)
errspend
plots=(asn power errspend)
;
TwoSidedAsymmetric: design nstages=4
method=errfuncgamma(gamma=1)
method(beta)=errfuncgamma(gamma=-2)
method(upperalpha)=errfuncgamma(gamma=-5)
alt=twosided
stop=both
beta=0.1
;
run;
The design uses gamma family error spending functions with 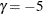 for the upper
for the upper  boundary,
boundary, 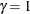 for the lower
for the lower  boundary, and
boundary, and 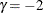 for the lower and upper
for the lower and upper 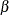 boundaries.
boundaries.
The "Design Information" table in Output 101.12.1 displays design specifications and the derived maximum information. Note that in order to attain the same information level
for the asymmetric lower and upper boundaries, the derived power at the upper alternative 0.93655 is larger than the specified
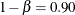 .
.
Output 101.12.1: Design Information
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Two-Sided |
| Early Stop | Accept/Reject Null |
| Method | Error Spending |
| Boundary Key | Both |
| Alternative Reference | 2 |
| Number of Stages | 4 |
| Alpha | 0.05 |
| Beta (Lower) | 0.1 |
| Beta (Upper) | 0.06345 |
| Power (Lower) | 0.9 |
| Power (Upper) | 0.93655 |
| Max Information (Percent of Fixed Sample) | 104.0688 |
| Max Information | 3.162386 |
| Null Ref ASN (Percent of Fixed Sample) | 74.16654 |
| Lower Alt Ref ASN (Percent of Fixed Sample) | 59.10271 |
| Upper Alt Ref ASN (Percent of Fixed Sample) | 73.78797 |
The "Method Information" table in Output 101.11.2 displays the specified  and
and 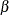 error levels and the derived drift parameter. With the same information level used for the asymmetric lower and upper boundaries,
only one of the
error levels and the derived drift parameter. With the same information level used for the asymmetric lower and upper boundaries,
only one of the 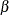 levels is maintained and the other is derived to have the level less than or equal to the specified level.
levels is maintained and the other is derived to have the level less than or equal to the specified level.
Output 101.12.2: Method Information
| Method Information | ||||||
|---|---|---|---|---|---|---|
| Boundary | Method | Alpha | Beta | Error Spending | Alternative Reference |
Drift |
| Function | ||||||
| Upper Alpha | Error Spending | 0.02500 | . | Gamma (Gamma=-5) | 2 | 3.55662 |
| Upper Beta | Error Spending | . | 0.06345 | Gamma (Gamma=-2) | 2 | 3.55662 |
| Lower Beta | Error Spending | . | 0.10000 | Gamma (Gamma=-2) | -2 | -3.55662 |
| Lower Alpha | Error Spending | 0.02500 | . | Gamma (Gamma=1) | -2 | -3.55662 |
With the STOPPROB(CREF=0 1) option, the "Expected Cumulative Stopping Probabilities" table in Output 101.12.3 displays the expected stopping stage and cumulative stopping probabilities at each stage under the null reference 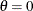 and under the alternative reference
and under the alternative reference 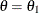 .
.
Output 101.12.3: Stopping Probabilities
| Expected Cumulative Stopping Probabilities Reference = CRef * (Alt Reference) |
|||||||
|---|---|---|---|---|---|---|---|
| CRef | Ref | Expected Stopping Stage |
Source | Stopping Probabilities | |||
| Stage_1 | Stage_2 | Stage_3 | Stage_4 | ||||
| 0.0000 | Lower Alt | 2.851 | Rej Null (Lower Alt) | 0.00875 | 0.01556 | 0.02087 | 0.02500 |
| 0.0000 | Lower Alt | 2.851 | Rej Null (Upper Alt) | 0.00042 | 0.00190 | 0.00704 | 0.02500 |
| 0.0000 | Lower Alt | 2.851 | Reject Null | 0.00917 | 0.01746 | 0.02791 | 0.05000 |
| 0.0000 | Lower Alt | 2.851 | Accept Null | 0.00000 | 0.30125 | 0.79354 | 0.95000 |
| 0.0000 | Lower Alt | 2.851 | Total | 0.00917 | 0.31870 | 0.82145 | 1.00000 |
| 1.0000 | Lower Alt | 2.272 | Rej Null (Lower Alt) | 0.27499 | 0.58934 | 0.79601 | 0.90000 |
| 1.0000 | Lower Alt | 2.272 | Rej Null (Upper Alt) | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 1.0000 | Lower Alt | 2.272 | Reject Null | 0.27499 | 0.58934 | 0.79601 | 0.90000 |
| 1.0000 | Lower Alt | 2.272 | Accept Null | 0.00000 | 0.01863 | 0.04935 | 0.10000 |
| 1.0000 | Lower Alt | 2.272 | Total | 0.27499 | 0.60797 | 0.84536 | 1.00000 |
| 0.0000 | Upper Alt | 2.851 | Rej Null (Lower Alt) | 0.00875 | 0.01556 | 0.02087 | 0.02500 |
| 0.0000 | Upper Alt | 2.851 | Rej Null (Upper Alt) | 0.00042 | 0.00190 | 0.00704 | 0.02500 |
| 0.0000 | Upper Alt | 2.851 | Reject Null | 0.00917 | 0.01746 | 0.02791 | 0.05000 |
| 0.0000 | Upper Alt | 2.851 | Accept Null | 0.00000 | 0.30125 | 0.79354 | 0.95000 |
| 0.0000 | Upper Alt | 2.851 | Total | 0.00917 | 0.31870 | 0.82145 | 1.00000 |
| 1.0000 | Upper Alt | 2.836 | Rej Null (Lower Alt) | 0.00002 | 0.00002 | 0.00002 | 0.00002 |
| 1.0000 | Upper Alt | 2.836 | Rej Null (Upper Alt) | 0.05945 | 0.33802 | 0.72323 | 0.93655 |
| 1.0000 | Upper Alt | 2.836 | Reject Null | 0.05947 | 0.33804 | 0.72325 | 0.93657 |
| 1.0000 | Upper Alt | 2.836 | Accept Null | 0.00000 | 0.01182 | 0.03131 | 0.06343 |
| 1.0000 | Upper Alt | 2.836 | Total | 0.05947 | 0.34986 | 0.75456 | 1.00000 |
"Rej Null (Lower Alt)" and "Rej Null (Upper Alt)" under the heading "Source" indicate the probabilities of rejecting the null hypothesis for the lower alternative and for the upper alternative, respectively. "Reject Null" indicates the probability of rejecting the null hypothesis for either the lower or upper alternative, "Accept Null" indicates the probability of accepting the null hypothesis, and "Total" indicates the total probability of stopping the trial.
With the PSS(CREF=0 0.5 1.0) option, the "Power and Expected Sample Sizes" table in Output 101.12.4 displays powers and expected sample sizes under hypothetical references 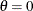 (null hypothesis
(null hypothesis 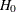 ),
), 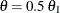 , and
, and 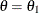 (alternative hypothesis
(alternative hypothesis 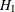 ), where
), where 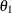 is the alternative reference. The expected sample sizes are displayed in a scale that indicates a percentage of its corresponding
fixed-sample size design.
is the alternative reference. The expected sample sizes are displayed in a scale that indicates a percentage of its corresponding
fixed-sample size design.
Output 101.12.4: Power and Expected Sample Size Information
| Powers and Expected Sample Sizes Reference = CRef * (Alt Reference) |
|||
|---|---|---|---|
| CRef | Ref | Power | Sample Size |
| Percent Fixed-Sample |
|||
| 0.0000 | Lower Alt | 0.02500 | 74.1665 |
| 0.5000 | Lower Alt | 0.34601 | 75.8425 |
| 1.0000 | Lower Alt | 0.90000 | 59.1027 |
| 0.0000 | Upper Alt | 0.02500 | 74.1665 |
| 0.5000 | Upper Alt | 0.41647 | 85.3976 |
| 1.0000 | Upper Alt | 0.93655 | 73.7880 |
Note that at 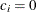 , the null reference
, the null reference 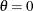 , the power with the lower alternative is the lower
, the power with the lower alternative is the lower  error 0.025, and the power with the upper alternative is the upper
error 0.025, and the power with the upper alternative is the upper  error 0.025. At
error 0.025. At 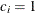 , the alternative reference
, the alternative reference 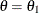 , the power with the lower alternative is the specified power 0.90, and the power with the upper alternative 0.93655 is greater
than the specified power 0.90 because the same information level is used for these two asymmetric boundaries.
, the power with the lower alternative is the specified power 0.90, and the power with the upper alternative 0.93655 is greater
than the specified power 0.90 because the same information level is used for these two asymmetric boundaries.
With the PLOTS=POWER option, the procedure displays a plot of the power curves under various hypothetical references, as shown
in Output 101.12.5. By default, powers under the lower hypotheses 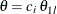 and under the upper hypotheses
and under the upper hypotheses 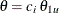 , are displayed for a two-sided asymmetric design, where
, are displayed for a two-sided asymmetric design, where 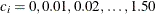 and
and 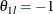 and
and 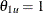 are the lower and upper alternative references, respectively.
are the lower and upper alternative references, respectively.
Output 101.12.5: Power Plot
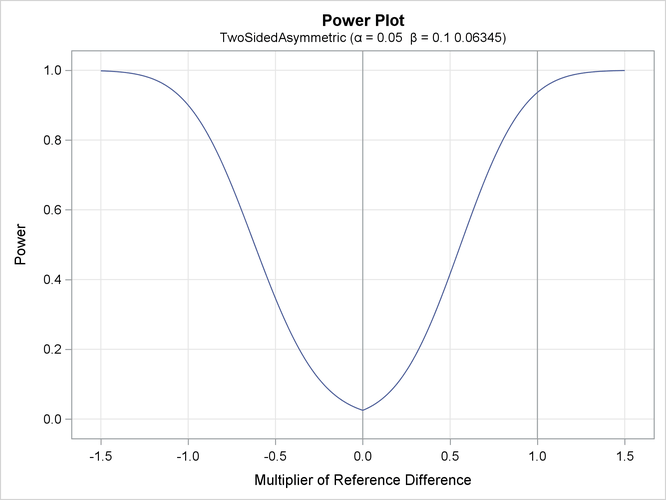
The horizontal axis displays the multiplier of the reference difference. A positive multiplier corresponds to 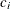 for the upper alternative hypothesis, and a negative multiplier corresponds to
for the upper alternative hypothesis, and a negative multiplier corresponds to 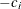 for the lower alternative hypothesis. For lower reference hypotheses, the power is the lower
for the lower alternative hypothesis. For lower reference hypotheses, the power is the lower  error 0.025 under the null hypothesis (
error 0.025 under the null hypothesis (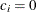 ) and is 0.90 under the alternative hypothesis (
) and is 0.90 under the alternative hypothesis (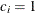 ). For upper reference hypotheses, the power is the upper
). For upper reference hypotheses, the power is the upper  error 0.025 under the null hypothesis (
error 0.025 under the null hypothesis (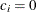 ) and is 0.93655 under the alternative hypothesis (
) and is 0.93655 under the alternative hypothesis (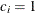 ).
).
With the PLOTS=ASN option, the procedure displays a plot of expected sample sizes under various hypothetical references, as
shown in Output 101.12.6. By default, expected sample sizes under the lower hypotheses 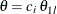 and under the upper hypotheses
and under the upper hypotheses 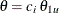 are displayed for a two-sided asymmetric design, where
are displayed for a two-sided asymmetric design, where 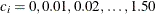 and
and 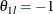 and
and 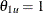 are the lower and upper alternative references, respectively.
are the lower and upper alternative references, respectively.
Output 101.12.6: ASN Plot
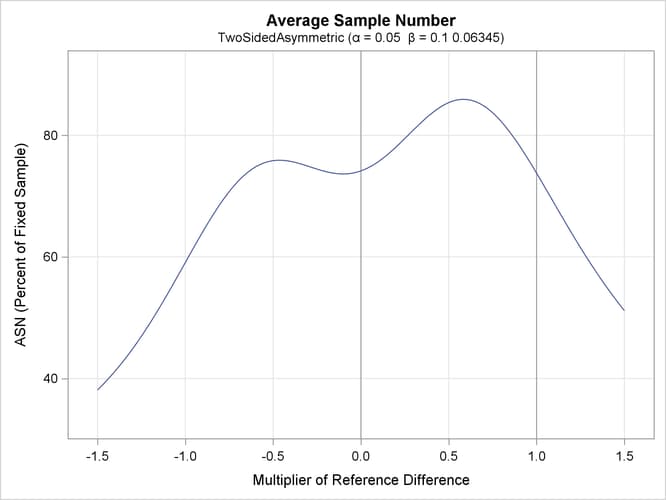
The horizontal axis displays the multiplier of the reference difference. A positive multiplier corresponds to 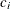 for the upper alternative hypothesis, and a negative multiplier corresponds to
for the upper alternative hypothesis, and a negative multiplier corresponds to 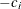 for the lower alternative hypothesis.
for the lower alternative hypothesis.
By default (or equivalently if you specify BETAOVERLAP=ADJUST), the SEQDESIGN procedure first derives boundary values without
adjusting for the possible overlapping of the two one-sided 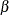 boundaries based on two corresponding one-sided tests. Then the procedure checks for overlapping of the
boundaries based on two corresponding one-sided tests. Then the procedure checks for overlapping of the 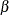 boundaries at the interim stages. Since the two
boundaries at the interim stages. Since the two 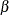 boundaries overlap at stage 1, the
boundaries overlap at stage 1, the 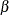 boundary values for stage 1 are set to missing, the
boundary values for stage 1 are set to missing, the 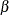 spending values at stage 1 are set to zero, and the
spending values at stage 1 are set to zero, and the 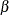 spending values at subsequent stages are adjusted proportionally.
spending values at subsequent stages are adjusted proportionally.
The "Boundary Information" table in Output 101.12.7 displays the information levels, alternative references, and boundary values. By default (or equivalently if you specify
BOUNDARYSCALE=STDZ), the standardized Z scale is used to display the alternative references and boundary values. The resulting standardized alternative references
at stage k is given by 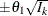 , where
, where 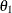 is the specified alternative reference and
is the specified alternative reference and 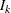 is the information level at stage k,
is the information level at stage k,  .
.
Output 101.12.7: Boundary Information
| Boundary Information (Standardized Z Scale) Null Reference = 0 |
||||||||
|---|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | ||||||
| Information Level | Reference | Lower | Upper | |||||
| Proportion | Actual | Lower | Upper | Alpha | Beta | Beta | Alpha | |
| 1 | 0.2500 | 0.790597 | -1.77831 | 1.77831 | -2.37610 | . | . | 3.33772 |
| 2 | 0.5000 | 1.581193 | -2.51491 | 2.51491 | -2.35714 | -0.48408 | 0.29400 | 2.94871 |
| 3 | 0.7500 | 2.37179 | -3.08012 | 3.08012 | -2.34861 | -1.36183 | 1.13898 | 2.50473 |
| 4 | 1.0000 | 3.162386 | -3.55662 | 3.55662 | -2.32105 | -2.32105 | 1.95675 | 1.95675 |
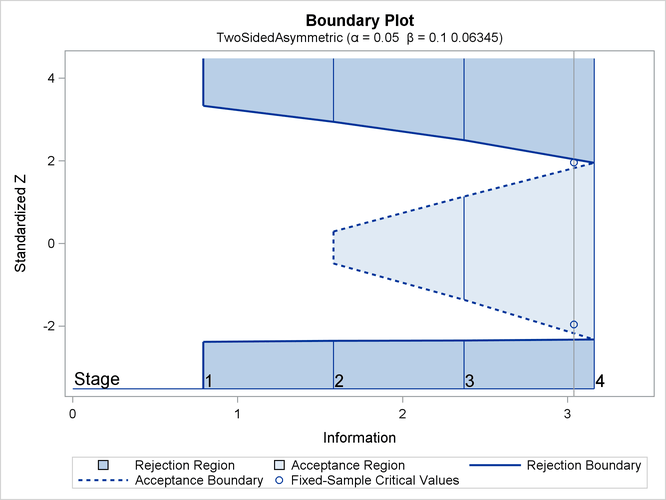
With ODS Graphics enabled, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 101.12.8.
Output 101.12.8: Boundary Plot
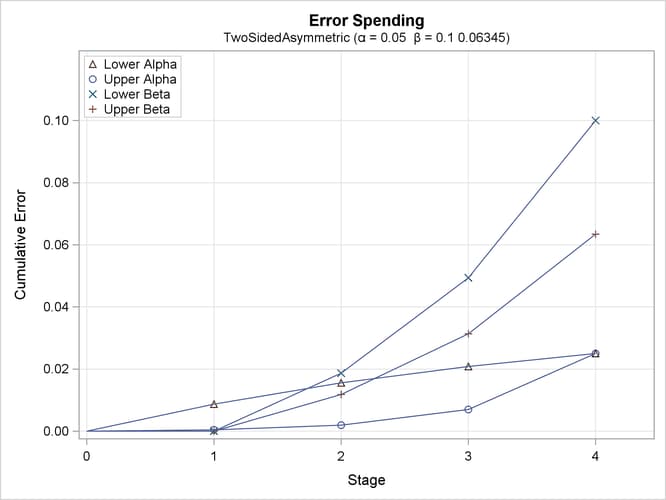
The "Error Spending Information" in Output 101.12.9 displays the cumulative error spending at each stage for each boundary.
Output 101.12.9: Error Spending Information
With the 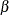 boundary values missing at stage 1, there is no early stopping to accept
boundary values missing at stage 1, there is no early stopping to accept 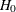 at stage 1, and the corresponding
at stage 1, and the corresponding 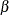 spending at stage 1 is computed from the rejection region. For example, the upper
spending at stage 1 is computed from the rejection region. For example, the upper 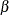 spending at stage 1 (0.00002) is the probability of rejecting
spending at stage 1 (0.00002) is the probability of rejecting 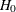 for the lower alternative under the upper alternative reference.
for the lower alternative under the upper alternative reference.
With the PLOTS=ERRSPEND option, the procedure displays a plot of the cumulative error spending on each boundary at each stage, as shown in Output 101.12.10.
Output 101.12.10: Error Spending Plot