The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
Fixed-Sample Clinical Trials
A clinical trial is a research study in consenting human beings to answer specific health questions. One type of trial is a treatment trial, which tests the effectiveness of an experimental treatment. An example is a planned experiment designed to assess the efficacy of a treatment in humans by comparing the outcomes in a group of patients who receive the test treatment with the outcomes in a comparable group of patients who receive a placebo control treatment, where patients in both groups are enrolled, treated, and followed over the same time period.
A clinical trial is conducted according to a plan called a protocol. The protocol provides detailed description of the study. For a fixed-sample trial, the study protocol contains detailed information such as the null hypothesis, the one-sided or two-sided test, and the Type I and II error probability levels. It also includes the test statistic and its associated critical values in the hypothesis testing.
Generally, the efficacy of a new treatment is demonstrated by testing a hypothesis 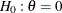 in a clinical trial, where
in a clinical trial, where 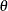 is the parameter of interest. For example, to test whether a population mean
is the parameter of interest. For example, to test whether a population mean 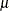 is greater than a specified value
is greater than a specified value 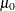 ,
, 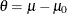 can be used with an alternative
can be used with an alternative 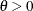 .
.
A one-sided test is a test of the hypothesis with either an upper (greater) or a lower (lesser) alternative, and a two-sided
test is a test of the hypothesis with a two-sided alternative. The drug industry often prefers to use a one-sided test to
demonstrate clinical superiority based on the argument that a study should not be run if the test drug would be worse (Chow,
Shao, and Wang 2003, p. 28). But in practice, two-sided tests are commonly performed in drug development (Senn 1997, p. 161). For a fixed Type I error probability  , the sample sizes required by one-sided and two-sided tests are different. See Senn (1997, pp. 161–167) for a detailed description of issues involving one-sided and two-sided tests.
, the sample sizes required by one-sided and two-sided tests are different. See Senn (1997, pp. 161–167) for a detailed description of issues involving one-sided and two-sided tests.
For independent and identically distributed observations 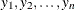 of a random variable, the likelihood function for
of a random variable, the likelihood function for 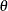 is
is
![\[ L(\theta ) = \prod _{j=1}^{n} L_{i} (\theta ) \]](images/statug_seqdesign0184.png)
where 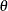 is the population parameter and
is the population parameter and 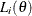 is the probability or probability density of
is the probability or probability density of 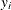 . Using the likelihood function, two statistics can be derived that are useful for inference: the maximum likelihood estimator
and the score statistic.
. Using the likelihood function, two statistics can be derived that are useful for inference: the maximum likelihood estimator
and the score statistic.
Maximum Likelihood Estimator
The maximum likelihood estimate (MLE)
of 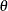 is the value
is the value 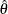 that maximizes the likelihood function for
that maximizes the likelihood function for 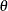 . Under mild regularity conditions,
. Under mild regularity conditions, 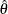 is an asymptotically unbiased estimate of
is an asymptotically unbiased estimate of 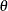 with variance
with variance 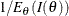 , where
, where 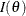 is the Fisher information
is the Fisher information
![\[ I(\theta ) = - \frac{ {\partial }^{2} \mr{log}( L(\theta ))}{\partial {\theta }^{2}} \]](images/statug_seqdesign0189.png)
and 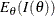 is the expected Fisher information (Diggle et al. 2002, p. 340)
is the expected Fisher information (Diggle et al. 2002, p. 340)
![\[ E_{\theta }( I(\theta ) ) = - E_{\theta } \left( \frac{ {\partial }^{2} \mr{log}( L(\theta ))}{\partial {\theta }^{2}} \right) \]](images/statug_seqdesign0191.png)
The score function for 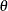 is defined as
is defined as
![\[ S( \theta ) = \frac{ \partial \, \mr{log}( L(\theta )) }{\partial \theta } \]](images/statug_seqdesign0192.png)
and usually, the MLE can be derived by solving the likelihood equation 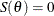 . Asymptotically, the MLE is normally distributed (Lindgren 1976, p. 272):
. Asymptotically, the MLE is normally distributed (Lindgren 1976, p. 272):
![\[ \hat{\theta } \sim N \left( \, \theta , \, \frac{1}{E_{\theta }( I(\theta ) )} \right) \]](images/statug_seqdesign0194.png)
If the Fisher information 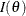 does not depend on
does not depend on 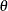 , then
, then 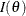 is known. Otherwise, either the expected information evaluated at the MLE
is known. Otherwise, either the expected information evaluated at the MLE 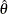 (
(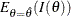 )
or the observed information
)
or the observed information 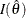 can be used for the Fisher information (Cox and Hinkley 1974, p. 302; Efron and Hinkley 1978, p. 458), where the observed Fisher information
can be used for the Fisher information (Cox and Hinkley 1974, p. 302; Efron and Hinkley 1978, p. 458), where the observed Fisher information
![\[ I({\hat{\theta }}) = - \left( \frac{ {\partial }^{2} \mr{log}( L(\theta )) }{ \partial {\theta }^{2} } \, | \, \theta ={\hat\theta } \right) \]](images/statug_seqdesign0197.png)
If the Fisher information 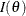 does depend on
does depend on 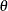 , the observed Fisher information is recommended for the variance of the maximum likelihood estimator (Efron and Hinkley 1978, p. 457).
, the observed Fisher information is recommended for the variance of the maximum likelihood estimator (Efron and Hinkley 1978, p. 457).
Thus, asymptotically, for large n,
![\[ \hat{\theta } \sim N \left( \, \theta , \, \frac{1}{I} \right) \]](images/statug_seqdesign0198.png)
where I is the information, either the expected Fisher information 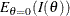 or the observed Fisher information
or the observed Fisher information 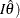 .
.
So to test 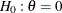 versus
versus 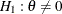 , you can use the standardized Z test statistic
, you can use the standardized Z test statistic
![\[ Z = \frac{\hat\theta }{\sqrt {\mr{Var}({\hat\theta })}} = {\hat\theta } \, \sqrt {I} \sim N \left( \, 0, \, 1 \right) \]](images/statug_seqdesign0201.png)
and the two-sided p-value is given by
![\[ \mr{Prob} (|Z| > |z_0|) = 1 - 2 \Phi (|z_0|) \]](images/statug_seqdesign0202.png)
where 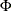 is the cumulative standard normal distribution function and
is the cumulative standard normal distribution function and 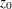 is the observed Z statistic.
is the observed Z statistic.
If the BOUNDARYSCALE=SCORE is specified in the SEQDESIGN procedure, the boundary values for the test statistic are displayed
in the score statistic scale. With the standardized Z statistic, the score statistic 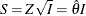 and
and
![\[ S \sim N \left( \, 0, \, I \right) \]](images/statug_seqdesign0205.png)
Score Statistic
The score statistic is based on the score function for 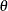 ,
,
![\[ S( \theta ) = \frac{ \partial \, \mr{log}( L(\theta )) }{\partial \theta } \]](images/statug_seqdesign0192.png)
Under the null hypothesis 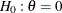 , the score statistic
, the score statistic 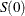 is the first derivative of the log likelihood evaluated at the null reference 0:
is the first derivative of the log likelihood evaluated at the null reference 0:
![\[ S(0) = \frac{ \partial \, \mr{log}( L(\theta )) }{\partial \theta } \, | \, \theta =0 \]](images/statug_seqdesign0207.png)
Under regularity conditions, 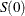 is asymptotically normally distributed with mean zero and variance
is asymptotically normally distributed with mean zero and variance 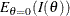 , the expected Fisher information evaluated at the null hypothesis
, the expected Fisher information evaluated at the null hypothesis 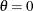 (Kalbfleisch and Prentice 1980, p. 45), where
(Kalbfleisch and Prentice 1980, p. 45), where 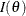 is the Fisher information
is the Fisher information
![\[ I(\theta ) = - E \left( \frac{ {\partial }^{2} \, \mr{log}( L(\theta )) }{ \partial {\theta }^{2} } \right) \]](images/statug_seqdesign0209.png)
That is, for large n,
![\[ S(0) \sim N \left( \, 0, \, E_{\theta =0} (I(\theta )) \right) \]](images/statug_seqdesign0210.png)
Asymptotically, the variance of the score statistic 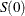 ,
, 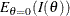 , can also be replaced by the expected Fisher information evaluated at the MLE
, can also be replaced by the expected Fisher information evaluated at the MLE 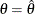 (
(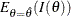 ),
the observed Fisher information evaluated at the null hypothesis
),
the observed Fisher information evaluated at the null hypothesis 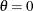 (
(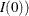 ,
or the observed Fisher information evaluated at the MLE
,
or the observed Fisher information evaluated at the MLE 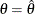 (
(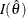 ) (Kalbfleisch and Prentice 1980, p. 46), where
) (Kalbfleisch and Prentice 1980, p. 46), where
![\[ I(0) = - \left( \frac{ {\partial }^{2} \mr{log}( L(\theta )) }{ \partial {\theta }^{2} } \, | \, \theta =0 \right) \]](images/statug_seqdesign0214.png)
![\[ I({\hat{\theta }}) = - \left( \frac{ {\partial }^{2} \mr{log}( L(\theta )) }{ \partial {\theta }^{2} } \, | \, \theta ={\hat\theta } \right) \]](images/statug_seqdesign0197.png)
Thus, asymptotically, for large n,
![\[ S(0) \sim N \left( \, 0, \, I \right) \]](images/statug_seqdesign0215.png)
where I is the information, either an expected Fisher information (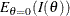 or
or 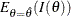 ) or a observed Fisher information (
) or a observed Fisher information (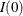 or
or 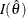 ).
).
So to test 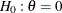 versus
versus 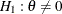 , you can use the standardized Z test statistic
, you can use the standardized Z test statistic
![\[ Z = \frac{S(0)}{\sqrt {I}} \]](images/statug_seqdesign0217.png)
If the BOUNDARYSCALE=MLE is specified in the SEQDESIGN procedure, the boundary values for the test statistic are displayed
in the MLE scale. With the standardized Z statistic, the MLE statistic 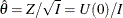 and
and
![\[ {\hat\theta } \sim N \left( \, 0, \, \frac{1}{I} \right) \]](images/statug_seqdesign0219.png)
One-Sample Test for Mean
The following one-sample test for mean is used to demonstrate fixed-sample clinical trials in the section One-Sided Fixed-Sample Tests in Clinical Trials and the section Two-Sided Fixed-Sample Tests in Clinical Trials.
Suppose 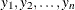 are n observations of a response variable
are n observations of a response variable Y from a normal distribution
![\[ y_{i} \sim N \left( \, \theta , \, {\sigma }^{2} \right) \]](images/statug_seqdesign0221.png)
where 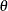 is the unknown mean and
is the unknown mean and 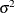 is the known variance.
is the known variance.
Then the log likelihood function for 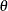 is
is
![\[ \mr{log} (L(\theta )) = \sum _{j=1}^{n} -\frac{1}{2} \frac{{(y_ j-\theta )}^{2}}{\sigma ^{2}} + c \]](images/statug_seqdesign0222.png)
where c is a constant. The first derivative is
![\[ \frac{ {\partial } \mr{log}( L(\theta )) }{ \partial {\theta } } = \frac{1}{\sigma ^{2}} \sum _{j=1}^{n} (y_ j - \theta ) = \frac{n}{\sigma ^{2}} ( {\overline{y}} - \theta ) \]](images/statug_seqdesign0223.png)
where 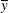 is the sample mean.
is the sample mean.
Setting the first derivative to zero, the MLE of 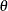 is
is 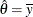 , the sample mean. The variance for
, the sample mean. The variance for 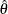 can be derived from the Fisher information
can be derived from the Fisher information
![\[ I(\theta ) = - \frac{ {\partial }^{2} \mr{log}( L(\theta )) }{ \partial {\theta }^{2} } = \frac{n}{\sigma ^{2}} \]](images/statug_seqdesign0226.png)
Since the Fisher information 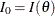 does not depend on
does not depend on 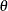 in this case,
in this case, 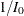 is used as the variance for
is used as the variance for 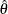 . Thus the sample mean
. Thus the sample mean 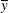 has a normal distribution with mean
has a normal distribution with mean 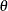 and variance
and variance 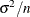 :
:
![\[ \hat{\theta } = {\overline{y}} \sim N \left( \, \theta , \, \frac{1}{I_{0}} \right) = N \left( \, \theta , \, \frac{{\sigma }^{2}}{n} \right) \]](images/statug_seqdesign0230.png)
Under the null hypothesis 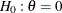 , the score statistic
, the score statistic
![\[ S(0) = \frac{ \partial \, \mr{log}( L(\theta )) }{\partial \theta } | \theta =0 = \frac{n}{\sigma ^{2}} {\overline{y}} \]](images/statug_seqdesign0231.png)
has a mean zero and variance
![\[ I(\theta ) = - \frac{ {\partial }^{2} \mr{log}( L(\theta )) }{ \partial {\theta }^{2} } = \frac{n}{\sigma ^{2}} \]](images/statug_seqdesign0226.png)
With the MLE 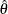 , the corresponding standardized statistic is computed as
, the corresponding standardized statistic is computed as 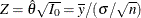 , which has a normal distribution with variance 1:
, which has a normal distribution with variance 1:
![\[ Z \sim N \left( \, {\theta } \sqrt {I_{0}}, \, 1 \right) = N \left( \, \frac{\theta }{\sigma / \sqrt {n}}, \, 1 \right) \]](images/statug_seqdesign0233.png)
Also, the corresponding score statistic is computed as 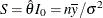 and
and
![\[ S \sim N \left( \, {\theta } I_{0}, \, I_{0} \right) = N \left( \, \frac{n \theta }{{\sigma }^{2}}, \, \frac{n}{{\sigma }^{2}} \right) \]](images/statug_seqdesign0235.png)
which is identical to 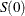 computed under the null hypothesis
computed under the null hypothesis 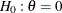 .
.
Note that if the variable Y does not have a normal distribution, then it is assumed that the sample size n is large such that the sample mean has an approximately normal distribution.