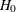The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
Whitehead Methods
The Whitehead methods (Whitehead and Stratton 1983; Whitehead 1997, 2001) derive boundary values by adjusting the boundary values generated from continuous monitoring. With continuous monitoring, the boundary values are on a straight line in the score scale for each boundary. For a group sequential design, the boundary values at an interim stage k depend on the information fractions
![\[ \Pi _{k} = \frac{I_{k}}{I_{X}} \]](images/statug_seqdesign0440.png)
where 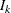 is the information available at stage k and
is the information available at stage k and 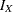 is the maximum information, the information available at the end of the trial if the trial does not stop early.
is the maximum information, the information available at the end of the trial if the trial does not stop early.
One-Sided Symmetric Designs
A one-sided symmetric design is a one-sided design with identical Type I and Type II error probabilities. For a one-sided
symmetric design with an upper alternative,  , the boundary values in the score scale from continuous monitoring are as follows:
, the boundary values in the score scale from continuous monitoring are as follows:
where  is the upper alternative reference,
is the upper alternative reference,  is a specified constant for the slope,
is a specified constant for the slope,  , and
, and  is a constant, fixed for STOP=BOTH and derived for STOP=ACCEPT and STOP=REJECT.
is a constant, fixed for STOP=BOTH and derived for STOP=ACCEPT and STOP=REJECT.
The upper 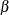 boundary value can also be expressed as
boundary value can also be expressed as
Thus, these straight-line boundaries form a triangle in the score statistic scale.
To adjust for the nature of discrete monitoring, the group sequential boundary values are given by the following:
where  and
and  ,
,  are the adjustments.
are the adjustments.
Note that with the adjustment  , the resulting boundaries form a Christmas tree shape within the original triangle and are referred to as the Christmas tree
boundaries (Whitehead 1997, p. 73).
, the resulting boundaries form a Christmas tree shape within the original triangle and are referred to as the Christmas tree
boundaries (Whitehead 1997, p. 73).
One-Sided Asymmetric Designs
For a one-sided asymmetric design with an upper alternative,  , the boundary values computed using the score scale, are given by the following:
, the boundary values computed using the score scale, are given by the following:
where  is the modified alternative reference
is the modified alternative reference
![\[ \tilde{{\theta }_{u}} = \frac{2 {\Phi }^{-1} (1-\alpha _ u)}{{\Phi }^{-1} (1-\alpha _ u) + {\Phi }^{-1} (1-\beta _ u)} \, {\theta }_{u} \]](images/statug_seqdesign0529.png)
The modified alternative reference  if
if  .
.
For a design with early stopping to reject or accept the null hypothesis,  , the boundary values at the final stage are equal. The modified drift parameter
, the boundary values at the final stage are equal. The modified drift parameter  is given by
is given by
![\[ \tilde{d}_{u} = \tilde{\theta }_{u} \sqrt {I_{X}} = \frac{1}{1 - 2 \tau _{u}} \left( \sqrt { {h_{K}}^{2} + 2 C_{u} (1 - 2 \tau _{u}) } - h_{K} \right) \]](images/statug_seqdesign0534.png)
where  .
.
A one-sided Whitehead design with early stopping to reject or accept the null hypothesis is illustrated in Example 101.7.
Two-Sided Designs
The boundary values for a two-sided design are generated by combining boundary values from two one-sided designs. With the STOP=BOTH option, this produces a double triangular design (Whitehead 1997, p. 98).
The boundary values for a two-sided design, using the score scale, are then given by the following:
where the modified alternative references are
![\[ \tilde{\theta }_{u} = \frac{2 {\Phi }^{-1} (1-\alpha _ u)}{{\Phi }^{-1} (1-\alpha _ u) + {\Phi }^{-1} (1-\beta _ u)} \, {\theta }_{u} \]](images/statug_seqdesign0540.png)
![\[ \tilde{\theta }_{l} = \frac{2 {\Phi }^{-1} (1-\alpha _ l)}{{\Phi }^{-1} (1-\alpha _ l) + {\Phi }^{-1} (1-\beta _ l)} \, {\theta }_{l} \]](images/statug_seqdesign0541.png)
The modified alternative reference  if
if  and
and  if
if  .
.
For a design with early stopping to reject or accept the null hypothesis, the two upper boundary values at the final stage
are identical and the two lower boundary values at the final stage are identical. That is,  and
and  . These modified drift parameters are then given by
. These modified drift parameters are then given by
![\[ \tilde{d}_{l} = \tilde{{\theta }}_{l} \sqrt {I_{X}} = \frac{1}{1 - 2 \tau _{l}} \left( \sqrt { {h_{K}}^{2} + 2 C_{l} (1 - 2 \tau _{l}) } - h_{K} \right) \]](images/statug_seqdesign0546.png)
![\[ \tilde{d}_{u} = \tilde{{\theta }}_{u} \sqrt {I_{X}} = \frac{1}{1 - 2 \tau _{u}} \left( \sqrt { {h_{K}}^{2} + 2 C_{u} (1 - 2 \tau _{u}) } - h_{K} \right) \]](images/statug_seqdesign0547.png)
where  .
.
For a design with early stopping to reject the null hypothesis, or a design with early stopping to accept the null hypothesis,
you can specify the slope parameters  and
and  in the TAU= option, and then the intercept parameters
in the TAU= option, and then the intercept parameters  and
and  , and the resulting boundary values are derived. If both the maximum information and alternative references are specified,
the procedure derives
, and the resulting boundary values are derived. If both the maximum information and alternative references are specified,
the procedure derives  and
and  by maintaining either the overall
by maintaining either the overall  levels (BOUNDARYKEY=ALPHA) or the overall
levels (BOUNDARYKEY=ALPHA) or the overall 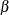 levels (BOUNDARYKEY=BETA). If the maximum information and alternative reference are not both specified, the procedure derives
the boundary values
levels (BOUNDARYKEY=BETA). If the maximum information and alternative reference are not both specified, the procedure derives
the boundary values  and
and  by maintaining both the overall
by maintaining both the overall  and overall
and overall 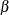 levels.
levels.
For a design with early stopping to reject or accept the null hypothesis (STOP=BOTH), Whitehead’s triangular test uses  and compute
and compute  and
and  for the boundary values. If the maximum information and alternative reference are both specified, the BOUNDARYKEY=ALPHA option
uses the specified
for the boundary values. If the maximum information and alternative reference are both specified, the BOUNDARYKEY=ALPHA option
uses the specified  values to compute the
values to compute the 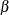 values and boundary values. The final-stage boundary values are modified to maintain the overall
values and boundary values. The final-stage boundary values are modified to maintain the overall  levels if they exist. Similarly, the BOUNDARYKEY=BETA option uses the specified
levels if they exist. Similarly, the BOUNDARYKEY=BETA option uses the specified 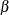 values to compute the
values to compute the  values and boundary values. The final-stage boundary values are modified to maintain the overall
values and boundary values. The final-stage boundary values are modified to maintain the overall 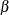 levels if they exist.
levels if they exist.
If the maximum information and alternative reference are not both specified, the specified  and
and 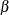 values are used to derive boundary values. The BOUNDARYKEY=NONE option uses these boundary values without adjustment. The
BOUNDARYKEY=ALPHA option modifies the final-stage boundary values to maintain the overall
values are used to derive boundary values. The BOUNDARYKEY=NONE option uses these boundary values without adjustment. The
BOUNDARYKEY=ALPHA option modifies the final-stage boundary values to maintain the overall  levels if they exist. Similarly, the BOUNDARYKEY=BETA option modifies the final-stage boundary values to maintain the overall
levels if they exist. Similarly, the BOUNDARYKEY=BETA option modifies the final-stage boundary values to maintain the overall
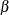 levels if they exist.
levels if they exist.
Applicable Boundary Keys
Table 101.7 lists applicable boundary keys for a design that uses Whitehead methods.
Table 101.7: Applicable Boundary Keys for Whitehead Methods
|
Specified Parameters |
Boundary Keys |
|||||||
|---|---|---|---|---|---|---|---|---|
|
Early Stopping |
(Alt Ref – Max Info) |
Tau |
Alpha |
Beta |
None |
Both |
||
|
Reject |
X |
X |
|
X |
X |
|||
|
Accept |
X |
X |
X |
X |
||||
|
Reject/Accept |
X |
0.25 |
X |
X |
||||
|
Reject |
X |
X |
||||||
|
Accept |
X |
X |
||||||
|
Reject/Accept |
0.25 |
X |
X |
X |
||||
Note that the symbol "X" under "(Alt Ref – Max Info)" indicates that both alternative reference and maximum information are specified.
For a design with early stopping to reject the null hypothesis, or a design with early stopping to accept the null hypothesis,
you can specify the slope parameter  in the TAU= option, and then the intercept parameter
in the TAU= option, and then the intercept parameter  and the resulting boundary values are derived. If both the maximum information and alternative reference are specified, the
procedure derives
and the resulting boundary values are derived. If both the maximum information and alternative reference are specified, the
procedure derives  by maintaining either the overall
by maintaining either the overall  levels (BOUNDARYKEY=ALPHA) or the overall
levels (BOUNDARYKEY=ALPHA) or the overall 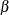 levels (BOUNDARYKEY=BETA). If the maximum information and alternative reference are not both specified, the procedure derives
the boundary values and
levels (BOUNDARYKEY=BETA). If the maximum information and alternative reference are not both specified, the procedure derives
the boundary values and  by maintaining both the overall
by maintaining both the overall  and overall
and overall 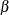 levels.
levels.
For a design with early stopping to reject or accept the null hypothesis (STOP=BOTH), Whitehead’s triangular test uses  and solves
and solves  for the boundary values. If the maximum information and alternative reference are both specified, the BOUNDARYKEY=ALPHA option
uses the specified
for the boundary values. If the maximum information and alternative reference are both specified, the BOUNDARYKEY=ALPHA option
uses the specified  value to compute the
value to compute the 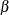 value and boundary values. The final-stage boundary value is modified to maintain the overall
value and boundary values. The final-stage boundary value is modified to maintain the overall  level if it exists. Similarly, the BOUNDARYKEY=BETA option uses the specified
level if it exists. Similarly, the BOUNDARYKEY=BETA option uses the specified 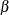 value to compute the
value to compute the  value and boundary values. The final-stage boundary value is modified to maintain the overall
value and boundary values. The final-stage boundary value is modified to maintain the overall 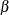 level if it exists.
level if it exists.
If the maximum information and alternative reference are not both specified, the specified  and
and 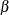 values are used to derive boundary values. The BOUNDARYKEY=NONE option uses these boundary values without adjustment. The
BOUNDARYKEY=ALPHA option modifies the final-stage boundary value to maintain the overall
values are used to derive boundary values. The BOUNDARYKEY=NONE option uses these boundary values without adjustment. The
BOUNDARYKEY=ALPHA option modifies the final-stage boundary value to maintain the overall  level if it exists. Similarly, the BOUNDARYKEY=BETA option modifies the final-stage boundary value to maintain the overall
level if it exists. Similarly, the BOUNDARYKEY=BETA option modifies the final-stage boundary value to maintain the overall
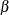 level if it exists.
level if it exists.