The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments -
Examples
 Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0 - References
Example 80.8 Creating a One-Sided Error Spending Design
This example requests a five-stage, one-sided group sequential design for normally distributed statistics. The design uses an O’Brien-Fleming-type error spending function for the  boundary and a Pocock-type error spending function for the
boundary and a Pocock-type error spending function for the 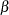 boundary. The following statements request a one-sided design by using different
boundary. The following statements request a one-sided design by using different  and
and 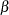 spending functions:
spending functions:
ods graphics on;
proc seqdesign altref=0.2 errspend
pss(cref=0 0.5 1)
stopprob(cref=0 0.5 1)
plots=(asn power errspend)
;
OneSidedErrorSpending: design nstages=5
method(alpha)=errfuncobf
method(beta)=errfuncpoc
alt=upper stop=both
alpha=0.025
;
run;
ods graphics off;
The "Design Information" table in Output 80.8.1 displays design specifications and the derived statistics. With the specified alternative reference, the maximum information is derived.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Method | Error Spending |
| Boundary Key | Both |
| Alternative Reference | 0.2 |
| Number of Stages | 5 |
| Alpha | 0.025 |
| Beta | 0.1 |
| Power | 0.9 |
| Max Information (Percent of Fixed Sample) | 119.4278 |
| Max Information | 313.7196 |
| Null Ref ASN (Percent of Fixed Sample) | 50.35408 |
| Alt Ref ASN (Percent of Fixed Sample) | 78.77223 |
The "Method Information" table in Output 80.8.2 displays the  and
and 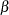 errors, alternative reference, and derived drift parameter, which is the standardized alternative reference at the final stage.
errors, alternative reference, and derived drift parameter, which is the standardized alternative reference at the final stage.
| Method Information | ||||||
|---|---|---|---|---|---|---|
| Boundary | Method | Alpha | Beta | Error Spending | Alternative Reference |
Drift |
| Function | ||||||
| Upper Alpha | Error Spending | 0.02500 | . | Approx O'Brien-Fleming | 0.2 | 3.542426 |
| Upper Beta | Error Spending | . | 0.10000 | Approx Pocock | 0.2 | 3.542426 |
With the STOPPROB option, the "Expected Cumulative Stopping Probabilities" table in Output 80.8.3 displays the expected stopping stage and cumulative stopping probability to reject the null hypothesis at each stage under various hypothetical references 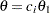 , where
, where 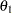 is the alternative reference and
is the alternative reference and  are values specified in the CREF= option.
are values specified in the CREF= option.
| Expected Cumulative Stopping Probabilities Reference = CRef * (Alt Reference) |
|||||||
|---|---|---|---|---|---|---|---|
| CRef | Expected Stopping Stage |
Source | Stopping Probabilities | ||||
| Stage_1 | Stage_2 | Stage_3 | Stage_4 | Stage_5 | |||
| 0.0000 | 2.108 | Reject Null | 0.00000 | 0.00039 | 0.00381 | 0.01221 | 0.02500 |
| 0.0000 | 2.108 | Accept Null | 0.38080 | 0.69133 | 0.86162 | 0.94170 | 0.97500 |
| 0.0000 | 2.108 | Total | 0.38080 | 0.69173 | 0.86543 | 0.95391 | 1.00000 |
| 0.5000 | 3.296 | Reject Null | 0.00002 | 0.01265 | 0.09650 | 0.24465 | 0.38724 |
| 0.5000 | 3.296 | Accept Null | 0.13665 | 0.28063 | 0.41080 | 0.52230 | 0.61276 |
| 0.5000 | 3.296 | Total | 0.13667 | 0.29328 | 0.50730 | 0.76695 | 1.00000 |
| 1.0000 | 3.298 | Reject Null | 0.00050 | 0.13209 | 0.52642 | 0.80390 | 0.90000 |
| 1.0000 | 3.298 | Accept Null | 0.02954 | 0.05231 | 0.07085 | 0.08648 | 0.10000 |
| 1.0000 | 3.298 | Total | 0.03004 | 0.18440 | 0.59728 | 0.89039 | 1.00000 |
With the PSS option, the "Power and Expected Sample Sizes" table in Output 80.8.4 displays powers and expected sample sizes under various hypothetical references 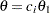 , where
, where 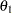 is the alternative reference and
is the alternative reference and  are the default values in the CREF= option.
are the default values in the CREF= option.
| Powers and Expected Sample Sizes Reference = CRef * (Alt Reference) |
||
|---|---|---|
| CRef | Power | Sample Size |
| Percent Fixed-Sample |
||
| 0.0000 | 0.02500 | 50.3541 |
| 0.5000 | 0.38724 | 78.7219 |
| 1.0000 | 0.90000 | 78.7722 |
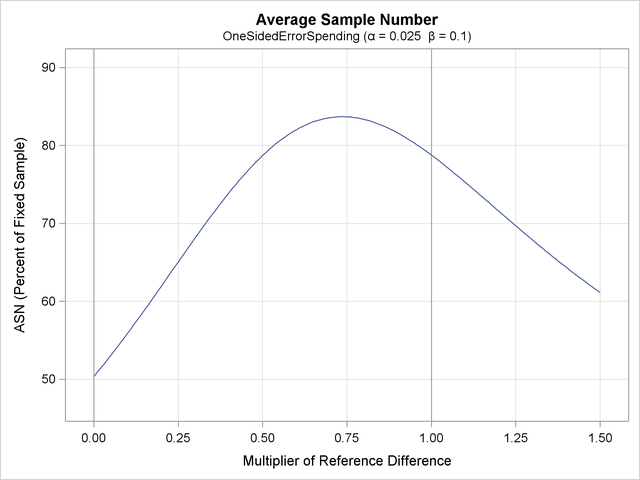
With the PLOTS=ASN option, the procedure displays a plot of expected sample sizes under various hypothetical references, as shown in Output 80.8.5. By default, expected sample sizes under the hypotheses  ,
,  , are displayed, where
, are displayed, where 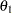 is the alternative reference.
is the alternative reference.
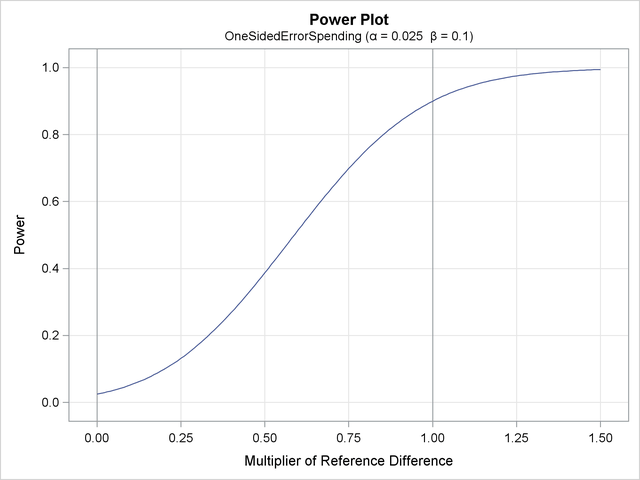
With the PLOTS=POWER option, the procedure displays a plot of the power curves under various hypothetical references for all designs simultaneously, as shown in Output 80.8.6. By default, the option CREF=  and powers under hypothetical references
and powers under hypothetical references  are displayed, where
are displayed, where  are values specified in the CREF= option. These CREF= values are displayed on the horizontal axis.
are values specified in the CREF= option. These CREF= values are displayed on the horizontal axis.
Under the null hypothesis, 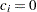 , the power is
, the power is 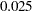 , the upper Type I error probability. Under the alternative hypothesis,
, the upper Type I error probability. Under the alternative hypothesis,  , the power is
, the power is 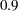 , one minus the Type II error probability. The plot shows only minor difference between the two designs.
, one minus the Type II error probability. The plot shows only minor difference between the two designs.
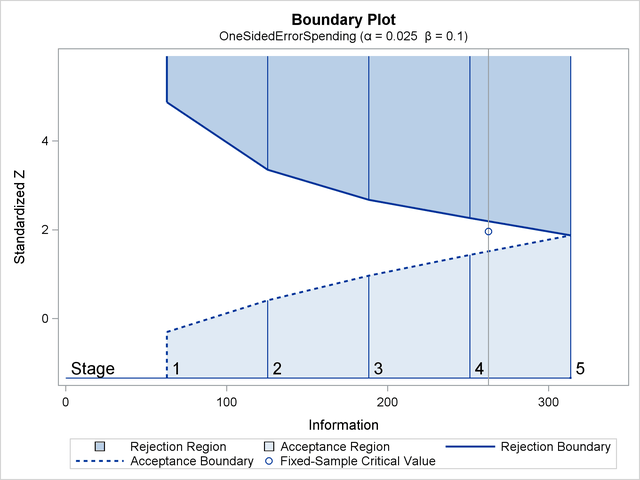
The "Boundary Information" table in Output 80.8.7 displays information level, alternative reference, and boundary values. By default (or equivalently if you specify BOUNDARYSCALE=STDZ), the alternative reference and boundary values are displayed with the standardized 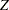 scale. That is, the resulting standardized alternative reference at stage
scale. That is, the resulting standardized alternative reference at stage  is given by
is given by 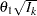 , where
, where 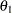 is the specified alternative reference and
is the specified alternative reference and 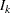 is the information level at stage
is the information level at stage  ,
,  .
.
| Boundary Information (Standardized Z Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | Upper | Beta | Alpha | |
| 1 | 0.2000 | 62.74393 | 1.58422 | -0.30338 | 4.87688 |
| 2 | 0.4000 | 125.4879 | 2.24043 | 0.41667 | 3.35706 |
| 3 | 0.6000 | 188.2318 | 2.74395 | 0.97165 | 2.67766 |
| 4 | 0.8000 | 250.9757 | 3.16844 | 1.43627 | 2.26535 |
| 5 | 1.0000 | 313.7196 | 3.54243 | 1.87522 | 1.87522 |
With ODS Graphics enabled, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 80.8.8. This plot displays the boundary values in the "Boundary Information" table in Output 80.8.7.
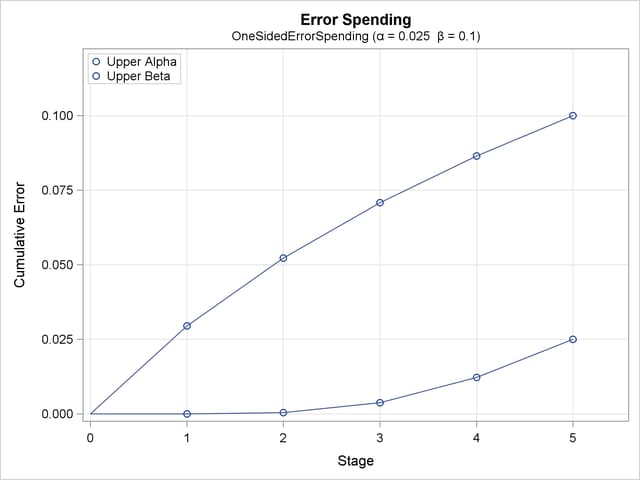
The "Error Spending Information" table in Output 80.8.9 displays cumulative error spending at each stage for each boundary.
| Error Spending Information | |||
|---|---|---|---|
| _Stage_ | Information Level |
Cumulative Error Spending | |
| Upper | |||
| Proportion | Beta | Alpha | |
| 1 | 0.2000 | 0.02954 | 0.00000 |
| 2 | 0.4000 | 0.05231 | 0.00039 |
| 3 | 0.6000 | 0.07085 | 0.00381 |
| 4 | 0.8000 | 0.08648 | 0.01221 |
| 5 | 1.0000 | 0.10000 | 0.02500 |
With the PLOTS=ERRSPEND option, the procedure displays a plot of error spending for each boundary, as shown in Output 80.8.10. This plot displays the cumulative error spending at each stage in the "Error Spending Information" table in Output 80.8.9. The O’Brien-Fleming-type  spending function is conservative in early stages because it uses much less at early stages than in the later stages. In contrast, the Pocock-type
spending function is conservative in early stages because it uses much less at early stages than in the later stages. In contrast, the Pocock-type 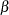 spending function uses more at early stages than in the later stages.
spending function uses more at early stages than in the later stages.