The SEQDESIGN Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
- References
| Summary of Methods in Group Sequential Designs |
There are three different types of methods available in the SEQDESIGN procedure: fixed boundary shape methods for specified boundary shape, Whitehead methods for boundaries from continuous monitoring, and error spending methods for specified error spending at each stage.
The fixed boundary shape methods include unified family methods and Haybittle-Peto methods. The unified family methods include Pocock, O’Brien-Fleming, power family, and triangular methods.
Pocock Method
Pocock derives the constant boundary on the standardized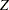 
scale to demonstrate the sequential design while maintaining the overall 
and 
levels (Pocock 1977). The resulting boundary tends to stop the trials early with a larger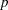 
-value. This boundary is commonly called a Pocock boundary, but Pocock himself does not advocate these boundary values for stopping a trial early to reject the null hypothesis, because large 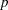-values might not be persuasive enough (Pocock and White 1999). Also, the nominal 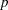-value at the final stage is much smaller than the overall 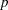-value of the design. That is, the trial might stop at the final stage with a small nominal 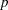-value, but the test is not rejected, which might not be easy to justify.
O’Brien-Fleming Method
O’Brien-Fleming boundary values are inversely proportional to the square root of information levels on the standardized 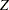scale (O’Brien and Fleming 1979). The O’Brien-Fleming boundary is conservative in the early stages and tends to stop the trials early only with a small 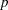-value. But the nominal value at the final stage is close to the overall 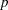-value of the design.
Power Family Method
The power family method (Wang and Tsiatis 1987; Emerson and Fleming 1989; Pampallona and Tsiatis 1994) generalizes the Pocock and O’Brien-Fleming methods with a power parameter to allow continuous movement between the Pocock and O’Brien-Fleming methods. The power parameter is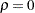 
for the Pocock method and 
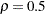for the O’Brien-Fleming method.
Triangular Method
The unified family triangular method (Kittelson and Emerson 1999) contains straight-line boundaries on the score scale. For a one-sided trial with early stopping either to reject and to accept the null hypothesis, the method produces a triangular continuation region. The boundary shape is specified with the slope parameter 
.
Unified Family Method
The unified family method (Kittelson and Emerson 1999) extends power family methods to incorporate the triangular method, which contains straight-line boundaries on the score scale.
Haybittle-Peto Method
The Haybittle-Peto method (Haybittle 1971; Peto et al. 1976) uses a 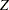value of 
for the critical values in interim stages and derives the critical value at the final stage. With this method, the final-stage critical value is close to the original design without interim monitoring. The SEQDESIGN procedure extends this method further to allow for different 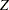or nominal 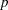-values for the boundaries.
Whitehead Method
Whitehead methods (Whitehead and Stratton 1983; Whitehead 1997, 2001) derive the boundary values by adapting the continuous monitoring tests to the discrete monitoring of group sequential tests. With early stopping to reject or accept the null hypothesis in a one-sided test, the derived continuation region has a triangular shape on the score-scaled boundaries. Only elementary calculations are needed to derive the boundary values in Whitehead’s triangular methods. The resulting Type I error probability and power are extremely close but differ slightly from the specified values due to the approximations used in deriving the tests (Jennison and Turnbull 2000, p. 106). The SEQDESIGN procedure provides the BOUNDARYKEY= option to adjust the boundary value at the final stage for the exact Type I or Type II error probability levels.
Error Spending Method
The error spending method uses the specified and errors to be used at each stage of the design to derive the boundary values.
Error Spending Function Method
The error spending function method uses the error spending function to compute the and errors to be used at each stage of the design and then to derive the boundary values for these errors. The following four error spending functions are available in the SEQDESIGN procedure:
The Pocock-type error spending function (Lan and DeMets 1983) produces boundaries similar to those produced with Pocock’s method.
The O’Brien-Fleming-type error spending function (Lan and DeMets 1983) produces boundaries similar to those produced with the O’Brien-Fleming method.
The gamma error spending function (Hwang, Shih, and DeCani 1990) specifies a gamma cumulative error spending function indexed by the gamma parameter
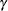. The boundaries created with 
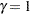are similar to the boundaries from the Pocock method, and the boundaries created with 
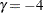or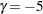 
are similar to the boundaries from the O’Brien-Fleming method. The power error spending function (Jennison and Turnbull 2000, p. 148) specifies a power cumulative error spending function indexed by the power parameter
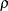. The boundaries created with 
are similar to the boundaries from the Pocock method, and the boundaries created with 
are similar to the boundaries from the O’Brien-Fleming method.