The SEQDESIGN Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
- References
| Boundary Scales |
The boundaries computed by the SEQDESIGN procedure are applied to test statistics computed during the analysis, and so generally, the scale you select for the boundaries is determined by the scale of the statistics that you will be using.
The following scales are available in the SEQDESIGN procedure:
These scales are all equivalent for a given set of boundary values—that is, there exists a unique transformation between any two of these scales. If you know the boundary values in terms of statistics from one scale, you can uniquely derive the boundary values of statistics for other scales. You can specify the scale with the BOUNDARYSCALE= option; the default is BOUNDARYSCALE=STDZ, the standardized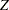 
scale.
You can also select the boundary scale to better examine the features of an individual group sequential design or to compare features among multiple designs. For example, with the standardized 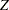scale, the boundary values for the Pocock design are identical across all stages, and the O’Brien-Fleming design has boundary values (in absolute value) that decrease over the stages.
The remaining section demonstrates the transformations from one scale to the other scales. If the maximum likelihood estimate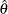 
is computed by the analysis, then
 |
where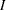 
is the Fisher information if it does not depend on 
. Otherwise, 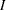is either the expected Fisher information evaluated at 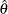or the observed Fisher information. See the section Maximum Likelihood Estimator for a detailed description of these statistics.
With the MLE statistic 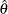, the corresponding standardized 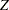statistic is computed as
 |
and the corresponding score statistic is computed as
 |
Similarly, if a score statistic 
is computed by the analysis, then with
 |
where 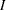is the information, either an expected Fisher information (
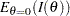or 
) or an observed Fisher information (
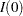or 
).
The corresponding standardized 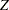statistic is computed as
 |
and the corresponding MLE-scaled statistic is computed as
 |
With a standardized normal 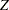statistic, the corresponding fixed-sample nominal 
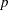-value depends on the type of alternative hypothesis. With an upper alternative, the nominal 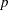-value is defined as the one-sided 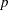-value under the null hypothesis 
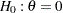with an upper alternative:
 |
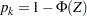With a lower alternative or a two-sided alternative, the nominal 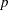-value is defined as the one-sided 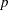-value under the null hypothesis 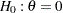with a lower alternative:
 |
which is an increasing function of the standardized 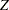statistic (Emerson, Kittelson, and Gillen 2005, p. 12).
The BOUNDARYSCALE= MLE, STDZ, SCORE, and PVALUE options display the boundary values in the MLE, standardize 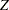, score, and 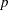-value scales, respectively. For example, suppose 
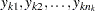are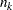 
observations of a response variable Y in a data set from a normal distribution with an unknown mean 
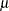and a known variance 
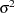. Then
 |
for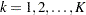 
, where 
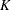is the number of groups and 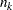is the number of observations at group 
.
If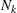 
is the cumulative number of observations for the first groups, then the sample mean from these 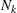observations
 |
has a normal distribution with mean and variance 
:
 |
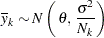To test the null hypothesis 
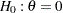, , where 
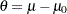can be used. The MLE of is 
and
 |
where the information is the inverse of the variance of 
,
 |
The corresponding standardized 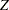statistic is
 |
The score statistic in the SEQDESIGN procedure is then given by
 |
For a null hypothesis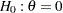 
with an upper alternative, the nominal 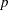-value of the standardized 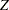statistic is 
. For a null hypothesis 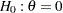with a lower alternative or a two-sided alternative, the nominal 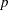-value of the standardized 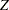statistic is 
.