The SEQDESIGN Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
- References
| One-Sided Fixed-Sample Tests in Clinical Trials |
A one-sided test has either an upper (greater) or a lower (lesser) alternative. This section describes one-sided tests with upper alternatives only. Corresponding results for one-sided tests with lower alternatives can be derived similarly.
For a one-sided test of 
with an upper alternative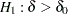 
, an equivalent null hypothesis is 
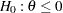with an upper alternative 
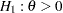, where 
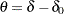. A fixed-sample test rejects 
if the standardized test statistic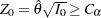 
, where 
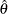is the sample estimate of 
and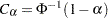 
is the critical value.
The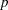 
-value of the test is given by 
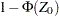, and the hypothesis is rejected if the 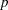-value is less than 
. An upper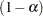 
confidence interval has the lower limit
 |
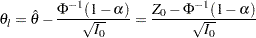The hypothesis is rejected if the confidence interval for the parameter does not contain zero—that is, if the lower limit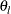 
is greater than 
.
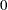With an alternative reference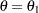 
, 
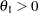, a Type II error probability is defined as
 |
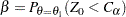which is equivalent to
 |
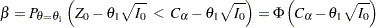Thus,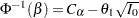 
. Then, with 
,
 |
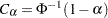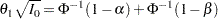The drift parameter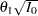 
can be computed for specified and 
and the maximum information is given by
 |
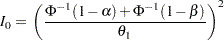If the maximum information is available, then the required sample size can be derived. For example, in a one-sample test for the mean with a specific standard deviation 
, the sample size 
required for the test is
 |
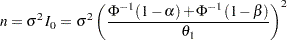On the other hand, if the alternative reference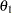 
, standard deviation , and sample size are all specified, then can be derived for a given and, similarly, can be derived for a given .
With an alternative reference 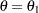, , 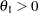the power 
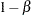is the probability of correctly rejecting the null hypothesis 
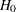at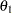 
:
 |
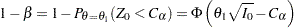Superiority Trials
A superiority trial that tests the response to a new drug is clinically superior to a comparative placebo control or active control therapy. If a positive value indicates a beneficial effect, a test for superiority has
 |
where is the hypothesis of nonsuperiority and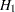 
is the alternative hypothesis of superiority.
The superiority test rejects the hypothesis and declares superiority if the standardized statistic 
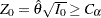, where the critical value .
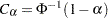For example, if is the response difference between the treatment and placebo control groups, then a superiority trial can be
 |
with a Type I error probability level 
and a power 
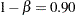at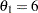 
.
Noninferiority Trials
A noninferiority trial does not compare the response to a new treatment with the response to a placebo. Instead, it demonstrates the effectiveness of a new treatment compared with that of a nonexisting placebo by showing that the response of a new treatment is not clinically inferior to the response of a standard therapy with an established effect. That is, this type of trial attempts to demonstrate that the new treatment effect is not worse than the standard therapy effect by an acceptable margin. These trials are often performed when there is an existing effective therapy for a serious disease, and therefore a placebo control group cannot be ethically included.
It can be difficult to specify an appropriate noninferiority margin. One practice is to choose with reference to the effect of the active control in historical placebo-controlled trials (Snapinn 2000, p. 20). With this practice, there is some basis to imply that the new treatment is better than the placebo for a positive noninferiority trial.
If a positive value indicates a beneficial effect, a test for noninferiority has a null hypothesis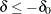 
and an alternative hypothesis 
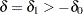, where 
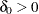is the specified noninferiority margin.
An equivalent test has
 |
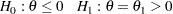where the parameter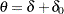 
, is the null hypothesis of inferiority, and 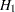is the alternative hypothesis of noninferiority,
The noninferiority test rejects the hypothesis and declares noninferiority if the standardized statistic 
, where the critical value .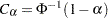
For example, if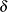 
is the response difference between the treatment and active control groups and 
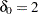is the noninferiority margin, then a noninferiority trial with a power 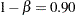at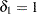 
might be
 |
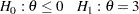where 
.