The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments -
Examples
 Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0 - References
Example 80.2 Creating a One-Sided O’Brien-Fleming Design
This example demonstrates a group sequential design for a clinical study. A clinic is conducting a study on the effect of vitamin C supplements in treating flu symptoms. The study groups consist of patients in the clinic with their first sign of flu symptoms within the last 24 hours. These individuals are randomly assigned to either the control group, which receives the placebo pills, or the treatment group, which receives large doses of vitamin C supplements. At the end of a five-day period, the flu symptoms of each individual are recorded.
Suppose that from past experience,  of individuals experiencing flu symptoms have the symptoms disappeared within five days. The clinic wants to detect a
of individuals experiencing flu symptoms have the symptoms disappeared within five days. The clinic wants to detect a  symptoms disappearance with a high probability in the trial. A test that compares the proportions directly is to specify a null hypothesis
symptoms disappearance with a high probability in the trial. A test that compares the proportions directly is to specify a null hypothesis  with a Type I error probability level
with a Type I error probability level  , where
, where 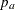 and
and 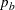 are the proportions of symptoms’ disappearance in the treatment group and control group, respectively. A one-sided alternative
are the proportions of symptoms’ disappearance in the treatment group and control group, respectively. A one-sided alternative 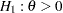 is also specified with a power of
is also specified with a power of 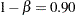 at
at 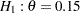 .
.
For a one-sided fixed-sample design, the critical value for the standardized 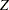 test statistic is given by
test statistic is given by 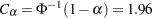 . That is, at the end of study, if the test statistic
. That is, at the end of study, if the test statistic  , then the null hypothesis is rejected and the efficacy of vitamin C supplements is declared. Otherwise, the null hypothesis is not rejected and the effect of vitamin C supplements is not significant.
, then the null hypothesis is rejected and the efficacy of vitamin C supplements is declared. Otherwise, the null hypothesis is not rejected and the effect of vitamin C supplements is not significant.
To achieve a 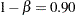 power at
power at 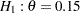 for a fixed-sample design, the information required is given by
for a fixed-sample design, the information required is given by
 |
With an equal sample size on the treatment and control groups,  , the sample size required for each group under
, the sample size required for each group under 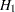 is computed from the information
is computed from the information 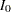 :
:
 |
where  and
and  are proportions in the treatment and control groups under
are proportions in the treatment and control groups under 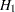 . That is,
. That is,
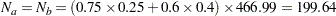 |
Thus,  individuals are required for each group in the fixed-sample study. See the section Test for the Difference between Two Binomial Proportions for a detailed derivation of these required sample sizes.
individuals are required for each group in the fixed-sample study. See the section Test for the Difference between Two Binomial Proportions for a detailed derivation of these required sample sizes.
Instead of a fixed-sample design for the trial, a group sequential design is used to stop the trial early for ethical concerns of possible harm or an unexpected strong efficacy outcome of the new drug. It can also save time and resources in the process. The following statements invoke the SEQDESIGN procedure and request a four-stage group sequential design that uses an O’Brien-Fleming method for normally distributed statistics. The design uses a one-sided alternative hypothesis 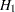 with early stopping to reject or accept
with early stopping to reject or accept  .
.
ods graphics on;
proc seqdesign altref=0.15
;
OneSidedOBrienFleming: design nstages=4
method=obf
alt=upper stop=both
alpha=0.025 beta=0.10
;
samplesize model=twosamplefreq(nullprop=0.6 test=prop);
ods output Boundary=Bnd_Prop;
run;
ods graphics off;
In a sequential design, a hypothesis can be rejected, accepted, or continued to the next time point at each interim stage. The STOP=BOTH option specifies early stopping to reject or accept the null hypothesis. The "Design Information," "Method Information," and "Boundary Information" tables are displayed by default.
The "Design Information" table in Output 80.2.1 displays design specifications and derived statistics such as power and maximum information. With a specified alternative reference, ALTREF=0.15, the maximum information 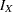 is derived.
is derived.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Method | O'Brien-Fleming |
| Boundary Key | Both |
| Alternative Reference | 0.15 |
| Number of Stages | 4 |
| Alpha | 0.025 |
| Beta | 0.1 |
| Power | 0.9 |
| Max Information (Percent of Fixed Sample) | 107.6741 |
| Max Information | 502.8343 |
| Null Ref ASN (Percent of Fixed Sample) | 61.12891 |
| Alt Ref ASN (Percent of Fixed Sample) | 75.89782 |
The Max Information (Percent Fixed-Sample) is the ratio in percentage between the maximum information for the group sequential design and the information required for a corresponding fixed-sample design:
 |
That is, if the group sequential trial does not stop at any interim stages, the information needed is  more than is needed for the corresponding fixed-sample design. For a two-sample test for binomial proportions, the information is proportional to the sample size. Thus,
more than is needed for the corresponding fixed-sample design. For a two-sample test for binomial proportions, the information is proportional to the sample size. Thus,  more observations are needed for the group sequential trial.
more observations are needed for the group sequential trial.
The Null Ref ASN (Percent Fixed-Sample) is the ratio in percentage between the expected sample size required under the null hypothesis for the group sequential design and the sample size required for the corresponding fixed-sample design. With a ratio of  , the expected sample size for the group sequential trial under the null hypothesis is
, the expected sample size for the group sequential trial under the null hypothesis is  of the sample size in the corresponding fixed-sample design.
of the sample size in the corresponding fixed-sample design.
Similarly, the Alt Ref ASN (Percent Fixed-Sample) is the ratio in percentage between the expected sample size required under the alternative hypothesis for the group sequential design and the sample size required for the corresponding fixed-sample design. With a ratio of 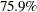 , the expected sample size for the group sequential trial under the alternative hypothesis is
, the expected sample size for the group sequential trial under the alternative hypothesis is 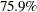 of the sample size in the corresponding fixed-sample design.
of the sample size in the corresponding fixed-sample design.
For a one-sided design with an upper alternative and early stopping to reject or accept the null hypothesis, upper  and
and  boundaries are created. The "Method Information" table in Output 80.2.2 displays the Type I error probability
boundaries are created. The "Method Information" table in Output 80.2.2 displays the Type I error probability  , the Type II error probability
, the Type II error probability  , and the derived drift parameter. The drift parameter is the standardized reference improvement between the alternative and null hypotheses at the final stage. It is also the standardized alternative reference at the final stage if the null reference is zero.
, and the derived drift parameter. The drift parameter is the standardized reference improvement between the alternative and null hypotheses at the final stage. It is also the standardized alternative reference at the final stage if the null reference is zero.
| Method Information | ||||||||
|---|---|---|---|---|---|---|---|---|
| Boundary | Method | Alpha | Beta | Unified Family | Alternative Reference |
Drift | ||
| Rho | Tau | C | ||||||
| Upper Alpha | O'Brien-Fleming | 0.02500 | . | 0.5 | 0 | 1.9784 | 0.15 | 3.363595 |
| Upper Beta | O'Brien-Fleming | . | 0.10000 | 0.5 | 0 | 1.3852 | 0.15 | 3.363595 |
With the METHOD=OBF option, the O’Brien-Fleming method is used for each boundary. The O’Brien-Fleming method is one of the unified family methods, and the "Method Information" table displays the corresponding parameter 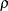 in the unified family method. The table also displays the critical values
in the unified family method. The table also displays the critical values  for the
for the  boundary and
boundary and 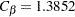 for the
for the  boundary. These critical values are used to create the boundary values.
boundary. These critical values are used to create the boundary values.
The "Boundary Information" table in Output 80.2.3 displays information level, alternative reference, and boundary values at each stage. By default (or equivalently if you specify BOUNDARYSCALE=STDZ), the alternative references and boundary values are displayed with the standardized 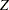 statistic scale. The resulting standardized alternative reference at stage
statistic scale. The resulting standardized alternative reference at stage 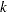 is given by
is given by 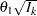 , where
, where 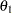 is the alternative reference and
is the alternative reference and 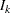 is the information level at stage
is the information level at stage 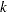 ,
, 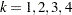 .
.
| Boundary Information (Standardized Z Scale) Null Reference = 0 |
||||||
|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | ||||
| Information Level | Reference | Upper | ||||
| Proportion | Actual | N | Upper | Beta | Alpha | |
| 1 | 0.2500 | 125.7086 | 107.4808 | 1.68180 | -1.08860 | 3.95679 |
| 2 | 0.5000 | 251.4171 | 214.9617 | 2.37842 | 0.41946 | 2.79788 |
| 3 | 0.7500 | 377.1257 | 322.4425 | 2.91296 | 1.31347 | 2.28446 |
| 4 | 1.0000 | 502.8343 | 429.9233 | 3.36360 | 1.97840 | 1.97840 |
By default (or equivalently if you specify INFO=EQUAL), equally spaced information levels are used. An information proportion is the proportion of maximum information available at each stage. With the derived maximum information, the actual information level at each stage is also displayed. With the SAMPLESIZE statement, the required sample size  is also displayed under the heading "Information Level."
is also displayed under the heading "Information Level."
At each interim stage, if the standardized 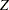 test statistic is larger than or equal to the corresponding upper
test statistic is larger than or equal to the corresponding upper  boundary, then the hypothesis
boundary, then the hypothesis 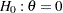 is rejected. If the test statistic is less than the corresponding upper
is rejected. If the test statistic is less than the corresponding upper  boundary, then the trial is stopped and the hypothesis
boundary, then the trial is stopped and the hypothesis  is accepted. Otherwise, the process continues to the next stage. At the final stage, stage
is accepted. Otherwise, the process continues to the next stage. At the final stage, stage 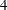 , the trial stops and the hypothesis
, the trial stops and the hypothesis  is rejected if the standardized
is rejected if the standardized 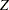 statistic
statistic  . Otherwise, the trial is accepted.
. Otherwise, the trial is accepted.
The ODS OUTPUT statement with the BOUNDARY=BND_PROP option creates an output data set that contains the resulting boundary information. After the actual data from the clinical trial are collected and analyzed at each stage with a procedure such as PROC GENMOD, the SEQTEST procedure is used to test the resulting statistics at stage  with the boundary information stored in the BOUND_PROP data set.
with the boundary information stored in the BOUND_PROP data set.
With ODS Graphics enabled, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 80.2.4.

The horizontal axis indicates the information levels for the design. The stages are indicated by vertical lines with accompanying stage numbers. If at any stage a test statistic is in a rejection region, the trial stops and the hypothesis is rejected. If a test statistic is in an acceptance region, then the trial also stops and the hypothesis is accepted. If the statistic is not in a rejection region or an acceptance region, the trial continues to the next stage. The boundary plot also displays the information level and critical value for the corresponding fixed-sample design.
The SEQDESIGN procedure derives the drift parameter 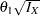 , where
, where 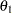 is the alternative reference and
is the alternative reference and 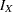 is the maximum information. If either
is the maximum information. If either 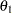 or
or 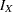 is specified, the other can be derived. With the SAMPLESIZE statement, the maximum information is used to compute the required sample size for the study.
is specified, the other can be derived. With the SAMPLESIZE statement, the maximum information is used to compute the required sample size for the study.
The "Sample Size Summary" table in Output 80.2.5 displays parameters for the sample size computation. With the MODEL=TWOSAMPLEFREQ( NULLPROP=0.6 TEST=PROP) option in the SAMPLESIZE statement, the total sample size in each group for testing the difference between two proportions is computed. By default (or equivalently if you specify REF=PROP in the MODEL=TWOSAMPLEFREQ option), the required sample sizes are computed under the alternative hypothesis. That is,
 |
where  and
and 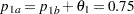 are the proportions in the control and treatment groups, respectively, under the alternative hypothesis
are the proportions in the control and treatment groups, respectively, under the alternative hypothesis 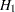 . See the section Test for the Difference between Two Binomial Proportions for a detailed description of these parameters.
. See the section Test for the Difference between Two Binomial Proportions for a detailed description of these parameters.
| Sample Size Summary | |
|---|---|
| Test | Two-Sample Proportions |
| Null Proportion | 0.6 |
| Proportion (Group A) | 0.75 |
| Test Statistic | Z for Proportion |
| Reference Proportions | Alt Ref |
| Max Sample Size | 429.9233 |
| Expected Sample Size (Null Ref) | 244.0768 |
| Expected Sample Size (Alt Ref) | 303.0464 |
The "Sample Sizes (N)" table in Output 80.2.6 displays the required sample sizes at each stage, in both fractional and integer numbers. The derived fractional sample sizes are under the heading "Fractional N." These sample sizes are rounded up to integers under the heading "Ceiling N." In practice, integer sample sizes are used, and the resulting information levels increase slightly. Thus,  ,
,  ,
,  , and
, and 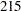 individuals are needed in each group for the four stages, respectively.
individuals are needed in each group for the four stages, respectively.
| Sample Sizes (N) Two-Sample Z Test for Proportion Difference |
||||||||
|---|---|---|---|---|---|---|---|---|
| _Stage_ | Fractional N | Ceiling N | ||||||
| N | N(Grp 1) | N(Grp 2) | Information | N | N(Grp 1) | N(Grp 2) | Information | |
| 1 | 107.48 | 53.74 | 53.74 | 125.7 | 108 | 54 | 54 | 126.3 |
| 2 | 214.96 | 107.48 | 107.48 | 251.4 | 216 | 108 | 108 | 252.6 |
| 3 | 322.44 | 161.22 | 161.22 | 377.1 | 324 | 162 | 162 | 378.9 |
| 4 | 429.92 | 214.96 | 214.96 | 502.8 | 430 | 215 | 215 | 502.9 |