The SEQDESIGN Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
- References
| Group Sequential Methods |
For a group sequential design, there are two possible boundaries for a one-sided test and four possible boundaries for a two-sided test. Each boundary consists of one boundary value (critical value) for each stage. The SEQDESIGN procedure provides various methods for computing the boundary values.
The boundary value for a fixed-sample test cannot be applied to each stage of sequential design because, as shown by Armitage, McPherson, and Rowe (1969), repeated significance tests at a fixed level on accumulating data increase the probability of a Type I error. For example, with a fixed-sample two-sided test, the critical values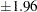 
for a standardized 
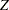statistic produce a Type I error probability level 
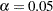. But for a two-sided group sequential test with two equally spaced stages, if the same critical values 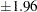are used to reject the null hypothesis at these two stages, the Type I error probability level is 
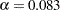, larger than the fixed-sample 
.
Numerous methods are available for deriving the critical values for each boundary in a sequential design. Pocock (1977) applies repeated significance tests to group sequential trials with equal-size groups and derives a constant critical value on the standardized normal 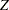scale across all stages that maintains the specified Type I error probability level. O’Brien and Fleming (1979) propose a sequential procedure that has boundary values (in absolute value) decrease over the stages on the standardized normal 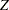scale.
The SEQDESIGN procedure provides the following three types of methods:
fixed boundary shape methods, which derive boundaries with specified boundary shapes
Whitehead methods, which adjust boundaries derived for continuous monitoring so that they apply to discrete monitoring
error spending methods
Each type of methods uses a distinct approach to derive the boundary values for a group sequential trial. Whitehead methods require much less computation with resulting Type I error probability and power that are close but differ slightly from the specified values due to the approximations used in deriving the tests (Jennison and Turnbull 2000, p. 106). Fixed boundary shape methods derive boundary values by estimating a fixed number of parameters and require more computation. Error spending methods derive boundary values at each stage sequentially and require much more computation than other types of methods for group sequential trials with a large number of stages.
Within each type of methods, you can choose methods that creating boundary values range from conservative stopping boundary values at early stages to liberal stopping boundary values at very early stages.
You can use the SEQDESIGN procedure to specify methods from the same type for each design. A different method can be specified for each boundary separately, but all methods in a design must be of the same type.
Fixed Boundary Shape Methods
The fixed boundary shape methods include the unified family methods and the Haybittle-Peto method. The unified family methods (Kittelson and Emerson 1999) derive boundaries from specified boundary shapes. These methods include Pocock’s method (Pocock 1977) and the O’Brien-Fleming method (O’Brien and Fleming 1979) as special cases.
The Haybittle-Peto method (Haybittle 1971; Peto et al. 1976) uses a value of 
for the critical values in interim stages, so the critical value at the final stage is close to the critical value for the fixed-sample design. In the SEQDESIGN procedure, the Haybittle-Peto method has been generalized to allow for different boundary values at interim stages.
Whitehead Methods
Whitehead and Stratton (1983) and Whitehead (1997, 2001) develop triangular and straight-line boundaries by adapting tests constructed for continuous monitoring to discrete monitoring of group sequential tests. With continuous monitoring, the values for each boundary fall in a straight line when plotted on the score statistic scale. The discrete boundary is derived by subtracting the expected overshoot from the continuous boundary to obtain the desired Type I and Type II error probabilities. For a design with early stopping to either reject or accept the null hypothesis, the boundaries form a triangle when plotted on the score statistic scale. See the section Score Statistic for a detailed description of the score statistic.
Error Spending Methods
For every sequential design, the and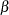 
errors at each stage can be computed from the boundary values. On the other hand, you can derive the boundary values from specified and 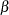errors for each stage. The error spending function approach (Lan and DeMets 1983) uses an error spending function to specify the errors at each stage for each boundary and then derives the boundary values.