The SEQDESIGN Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
- References
| Type I and Type II Errors |
The Type I error is the error of rejecting the null hypothesis when the null hypothesis is correct, and the Type II error is the error of not rejecting the null hypothesis when the null hypothesis is incorrect. The level of significance 
is the probability of making a Type I error. The Type II error depends on the hypothetical reference of the alternative hypothesis, and the Type II error probability 
is defined as the probability of not rejecting the null hypothesis when a specific alternative reference is true. The power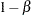 
is then defined as the probability of rejecting the null hypothesis at the alternative reference.
In a sequential design, if the maximum information and alternative reference are not both specified, the critical values are created such that both the specified Type I and the specified Type II error probability levels are maintained in the design. Otherwise, the critical values are created such that either the specified Type I error probability or the specified Type II error probability is maintained.
One-Sided Tests
For a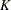 
-stage group sequential design with an upper alternative hypothesis 
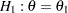and early stopping to reject or accept the null hypothesis 
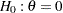, the boundaries contain the upper critical values 
and upper critical values 
, 
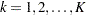. At each interim stage, 
, the null hypothesis 
is rejected if the observed statistic 
, is accepted if 
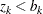, or the process is continued to the next stage if 
. At the final stage 
, the hypothesis is either rejected or accepted.
The overall Type I error probability is given by
 |
where 
is the spending at stage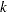 
. That is, at stage 
,
 |
At a subsequent stage ,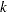
 |
Similarly, the Type II error probability
 |
where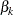 
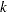is the spending at stage . That is, at stage ,
 |
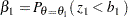At a subsequent stage ,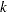
 |
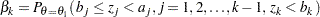With an upper alternative hypothesis 
, the power 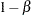is the probability of rejecting the null hypothesis for the upper alternative.
 |
For a design with early stopping to reject only, the interim upper critical values are set to 
, 
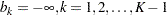, and 
. For a design with early stopping to accept only, the interim upper critical values are set to 
, 
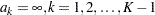, and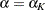 
.
Similarly, the Type I and Type II error probabilities for a 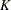-stage design with a lower alternative hypothesis 
can also be derived.
Two-Sided Tests
For a 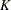-stage group sequential design with two-sided alternative hypotheses 
and 
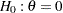, and early stopping to reject or accept the null hypothesis , the boundaries contain the upper critical values , upper critical values , lower critical values 
, and lower critical values 
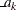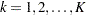, . At each interim stage, 
, the null hypothesis is rejected if the observed statistic or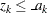 
, is accepted if 
, or the process is continued to the next stage if or 
. At the final stage and 
, the hypothesis is either rejected or accepted.
The overall upper Type I error probability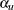 
is given by
 |
where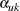 
is the spending at stage 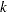for the upper alternative. That is, at stage ,
 |
At a subsequent stage ,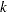
 |
Similarly, the overall lower Type I error probability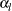 
can also be derived, and the overall Type I error probability 
.
The overall upper Type II error probability 
is given by
 |
where 
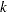is the upper spending at stage . That is, at stage ,
 |
At a subsequent stage ,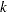
 |
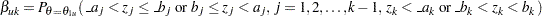With an upper alternative hypothesis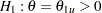 
, the power 
is the probability of rejecting the null hypothesis for the upper alternative:
 |
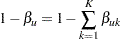which is
 |
The overall lower Type II error probability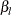 
and power 
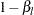can be similarly derived.
For a design with early stopping only to reject , both the interim lower and upper critical values are set to missing,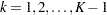 
, and 
, 
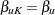. For a design with early stopping only to accept , the interim upper critical values are set to , 
, and the interim lower critical values are set to , 
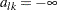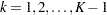, , and 
, 
.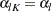