The SEQDESIGN Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
- References
| Group Sequential Methods |
A group sequential design provides interim analyses before the formal completion of a trial. The monitoring process provides possible early stopping for either positive or negative results and thus reduces the time to complete the trial. With a specified number of stages, the design creates critical values such that at each interim analysis, a hypothesis can be rejected, accepted, or continued to the next time point. At the final stage, a hypothesis is either rejected or accepted. Usually, the critical values are derived such that the specified overall Type I and Type II error probability levels are maintained in the design.
For example, to test a null hypothesis 
with an upper alternative in a fixed-sample design, a critical value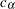 
is created. The null hypothesis is rejected if the test statistic is greater than or equal to the critical value 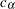. Otherwise, is accepted. But, for a group sequential design with early stopping to reject or accept the null hypothesis , there are two critical values created at each interim analysis: an 
critical value 
to reject the null hypothesis and a 
critical value 
to accept the null hypothesis. The null hypothesis is rejected if the test statistic is greater than or equal to the critical value , and is accepted if the test statistic is less than the critical value . If the test statistic is between these two critical values, the process continues to the next stage. At the final stage, the two critical values are equal, and the hypothesis is either rejected or accepted.
Armitage, McPherson, and Rowe (1969) showed that repeated significance tests at a fixed level on accumulating data increase the probability of obtaining a significant result under the null hypothesis. For example, with a significance level 
in a two-sided fixed-sample test, the critical value is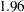 
. If this value is used in a five-stage group sequential trial with early stopping to reject the null hypothesis, then the probability of rejecting the null hypothesis at or before the fifth stage is 
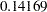, much larger than the nominal value (Armitage, McPherson, and Rowe 1969, p. 239).
Pocock (1977) applied these repeated significance tests to group sequential trials with equally spaced information levels and derives a constant critical value on the standardized normal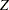 
scale across all stages that maintains the Type I error probability level. For example, with a significance level in a two-sided test, the derived critical value at each stage is 
on the standardized normal 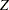scale, larger than the fixed-sample critical value 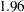. The corresponding nominal 
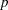-value is 
, which is smaller than the fixed-sample 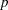-value 
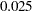(Pocock 1977, p. 193).
O’Brien and Fleming (1979) proposed a sequential procedure that has boundary values decrease over the stages on the standardized normal 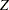scale to make the early stop less likely. The procedure has conservative stopping boundary values at very early stages, and boundary values at the final stage are close to the fixed-sample design. For example, with a significance level in a two-sided test, the derived critical values at these five stages on the standardized normal 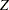scale are 
, 
, 
, 
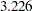, and 
.
Wang and Tsiatis (1987), Emerson and Fleming (1989) and Pampallona and Tsiatis (1994) generalized the Pocock and O’Brien-Fleming methods to the power family, where a power parameter is used to allow a continuous set of designs between the Pocock and O’Brien-Fleming methods.
Kittelson and Emerson (1999) extended the methods in the power family even further to the unified family, which also includes the exact triangular method. The shape and location of each of the four boundaries can be independently specified in the unified family methods.
Whitehead and Stratton (1983) and Whitehead (1997, 2001) developed triangular methods by adapting tests for continuous monitoring to discrete monitoring. With early stopping to reject or accept the null hypothesis in a one-sided test, the derived continuation region has a triangular shape for the score-scaled boundaries. Only elementary calculations are needed to derive the boundary values for Whitehead’s triangular methods.
For a sequential design, you can derive the and error probabilities at each stage from the boundaries. On the other hand, you can derive the boundaries from specified and error probabilities at each stage. The error spending function approach (Lan and DeMets 1983) uses the error spending function to specify the error probabilities at each stage and then uses these probabilities to derive the boundaries. You can specify and explicitly or implicitly with an error spending function for the cumulative probabilities.
Refer to Jennison and Turnbull (2000, pp. 5–11) for a more detailed history of group sequential methods.
The following three types of methods are available in the SEQDESIGN procedure to derive boundaries in a sequential design:
fixed boundary shape methods, which derive boundaries with specified boundary shapes. These include the unified family method and Haybittle-Peto method.
Whitehead methods, which adjust the boundaries from continuous monitoring for discrete monitoring
error spending methods
You can use the SEQDESIGN procedure to specify methods from the same group for each design. A different method can be specified for each boundary separately, but all methods in a design must be from the same group.
Fixed Boundary Shape Methods
The fixed boundary shape methods include the unified family method (Kittelson and Emerson 1999) and the Haybittle-Peto method (Haybittle 1971; Peto et al. 1976). The unified family methods derive the boundary values with the specified boundary shape. The unified family methods include the Pocock method (Pocock 1977), the O’Brien-Fleming method (O’Brien and Fleming 1979), the power family method (Wang and Tsiatis 1987; Emerson and Fleming 1989; Pampallona and Tsiatis 1994), and the triangular method (Kittelson and Emerson 1999). See the section Unified Family Methods for a detailed description of the methods that use the unified family approach.
The Haybittle-Peto method uses a value of 
for the critical values in interim stages, so that the critical value at the final stage is close to the original design without interim monitoring. In the SEQDESIGN procedure, the Haybittle-Peto method has been generalized to allow for different boundary values at different stages. See the section Haybittle-Peto Method for a detailed description of the Haybittle-Peto method.
Whitehead Methods
The Whitehead methods (Whitehead and Stratton 1983; Whitehead 1997, 2001) derive the boundary values by adapting the continuous monitoring tests to the discrete monitoring of group sequential tests. The Type I error probability and power corresponding to the resulting boundaries are extremely close but differ slightly from the specified values because of the approximations used in deriving the tests (Jennison and Turnbull 2000, p. 106). The SEQDESIGN procedure provides the BOUNDARYKEY= option to adjust the boundary value at the final stage for the exact Type I or Type II error probability level. See the section Whitehead Methods for a detailed description of Whitehead’s methods.
Error Spending Methods
An error spending method (Lan and DeMets 1983) uses the error spending function to specify the error spending at each stage and then uses these error probabilities to derive the boundary values. You can specify these errors explicitly or with an error spending function for these cumulative errors. See the section Error Spending Methods for a detailed description of the error spending methods.
Error spending methods derive boundary values at each stage sequentially and require much more computation than other types of methods for group sequential trials with a large number of stages, especially for a two-sided asymmetric design with early stopping to accept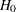 
, or to reject or accept .
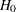The sample size requirement for some applicable tests can also be computed in the procedure. After the actual data from a clinical trial are collected, you can then use the boundary information created in the SEQDESIGN procedure to perform a group sequential test in the SEQTEST procedure.