The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
Fixed-Sample Clinical Trials One-Sided Fixed-Sample Tests in Clinical Trials Two-Sided Fixed-Sample Tests in Clinical Trials Group Sequential Methods Statistical Assumptions for Group Sequential Designs Boundary Scales Boundary Variables Type I and Type II Errors Unified Family Methods Haybittle-Peto Method Whitehead Methods Error Spending Methods Acceptance (beta) Boundary Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Specified and Derived Parameters Applicable Boundary Keys Sample Size Computation Applicable One-Sample Tests and Sample Size Computation Applicable Two-Sample Tests and Sample Size Computation Applicable Regression Parameter Tests and Sample Size Computation Aspects of Group Sequential Designs Summary of Methods in Group Sequential Designs Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments -
Examples
 Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0
Creating Fixed-Sample Designs Creating a One-Sided O’Brien-Fleming Design Creating Two-Sided Pocock and O’Brien-Fleming Designs Generating Graphics Display for Sequential Designs Creating Designs Using Haybittle-Peto Methods Creating Designs with Various Stopping Criteria Creating Whitehead’s Triangular Designs Creating a One-Sided Error Spending Design Creating Designs with Various Number of Stages Creating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta Boundaries Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0 Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0 - References
| Sample Size Computation |
The SEQDESIGN procedure assumes that the data are from a multivariate normal distribution and the sequence of the standardized test statistics 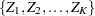 has the following canonical joint distribution:
has the following canonical joint distribution:
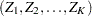 is multivariate normal
is multivariate normal 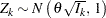
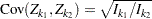 ,
, 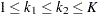
where 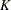 is the total number of stages and
is the total number of stages and 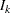 is the information available at stage
is the information available at stage 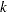 .
.
If the test statistic is computed from the data that are not from a normal distribution, such as a binomial distribution, then it is assumed that the test statistic is computed from a large sample such that the statistic has an approximately normal distribution.
In a typical clinical trial, the sample size required depends on the Type I error probability level  , alternative reference
, alternative reference 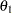 , power
, power 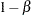 , and variance of the response variable. Given a one-sided null hypothesis
, and variance of the response variable. Given a one-sided null hypothesis 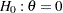 with an upper alternative hypothesis
with an upper alternative hypothesis  , the information required for a fixed-sample test is given by
, the information required for a fixed-sample test is given by
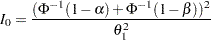 |
The parameter  and the subsequent alternative reference
and the subsequent alternative reference 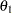 depend on the test specified in the clinical trial. For example, suppose you are comparing two binomial populations
depend on the test specified in the clinical trial. For example, suppose you are comparing two binomial populations 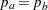 ; then
; then  is the difference between two proportions if the proportion difference statistic is used, and
is the difference between two proportions if the proportion difference statistic is used, and 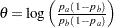 , the log odds ratio for the two proportions if the log odds ratio statistic is used.
, the log odds ratio for the two proportions if the log odds ratio statistic is used.
If the maximum likelihood estimate 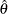 from the likelihood function can be derived, then the asymptotic variance for
from the likelihood function can be derived, then the asymptotic variance for 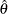 is
is 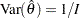 , where
, where 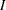 is Fisher information for
is Fisher information for  . The resulting statistic
. The resulting statistic 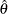 corresponds to the MLE statistic scale as specified in the BOUNDARYSCALE=MLE option in the PROC SEQDESIGN statement,
corresponds to the MLE statistic scale as specified in the BOUNDARYSCALE=MLE option in the PROC SEQDESIGN statement, 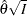 corresponds to the standardized
corresponds to the standardized 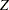 scale (BOUNDARYSCALE=STDZ), and
scale (BOUNDARYSCALE=STDZ), and 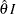 corresponds to the score statistic scale (BOUNDARYSCALE=SCORE).
corresponds to the score statistic scale (BOUNDARYSCALE=SCORE).
Alternatively, if the score statistic  is derived in a statistical procedure, it can be used as the test statistic and its asymptotic variance is given by Fisher information,
is derived in a statistical procedure, it can be used as the test statistic and its asymptotic variance is given by Fisher information, 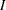 . In this case,
. In this case, 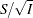 corresponds to the standardized
corresponds to the standardized 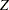 scale and
scale and 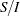 corresponds to the MLE statistic scale.
corresponds to the MLE statistic scale.
For a group sequential trial, the maximum information 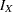 is derived in the SEQDESIGN procedure with the specified
is derived in the SEQDESIGN procedure with the specified  ,
,  , and
, and 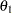 . With the maximum information
. With the maximum information
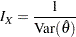 |
the sample size required for a specified test statistic in the trial can be evaluated or estimated from the known or estimated variance of the response variable. Note that different designs might produce different maximum information levels for the same hypothesis, and this in turn might require a different number of observations for the trial.
If each observation in the data set provides one unit of information in a hypothesis testing, such as a one-sample test for the mean, the required sample size for the sequential design can be derived from the maximum information. However, for a survival analysis, an individual in the survival time data might provide only partial information because of censoring. In this case, the required number of events can be derived from the maximum information. With addition accrual information, the sample size can also be computed.
The SEQDESIGN procedure provides sample size computation for some one-sample and two-sample tests in the SAMPLESIZE statement. It also provides sample size computation for tests of a parameter in regression models such as normal regression, logistic regression, and proportional hazards regression. In addition, the procedure can also compute the required sample size or number of events from the corresponding number in the fixed-sample design.
Table 80.11 lists the options available in the SAMPLESIZE statement.
Option |
Description |
|---|---|
Fixed-Sample Models |
|
INPUTNOBS |
specifies sample size for fixed-sample design |
INPUTNEVENTS |
specifies number of events for fixed-sample design |
One-Sample Models |
|
ONESAMPLEMEAN |
specifies one-sample |
ONESAMPLEFREQ |
specifies one-sample test for binomial proportion |
Two-Sample Models |
|
TWOSAMPLEMEAN |
specifies two-sample |
TWOSAMPLEFREQ |
specifies two-sample test for binomial proportions |
TWOSAMPLESURVIVAL |
specifies log-rank test for two survival distributions |
Regression Models |
|
REG |
specifies test for a regression parameter |
LOGISTIC |
specifies test for a logistic regression parameter |
PHREG |
specifies test for a proportional hazards regression parameter |
The MODEL=INPUTNOBS and MODEL=INPUTNEVENTS options are described next, and the remaining options are described in the next three sections.
Input Sample Size for Fixed-Sample Design
The MODEL=INPUTNOBS option derives the sample size required for a group sequential trial from the sample size 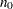 for the corresponding fixed-sample design. With the N=
for the corresponding fixed-sample design. With the N= 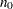 option specifying the sample size
option specifying the sample size 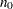 for a fixed-sample design, the sample size required for a group sequential trial is then computed as
for a fixed-sample design, the sample size required for a group sequential trial is then computed as
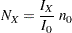 |
where 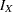 is the maximum information for the group sequential design and
is the maximum information for the group sequential design and 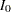 is the information for the corresponding fixed-sample design. The information ratio between
is the information for the corresponding fixed-sample design. The information ratio between 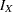 and
and 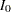 is derived in the SEQDESIGN procedure.
is derived in the SEQDESIGN procedure.
The SAMPLE=ONE option specifies a one-sample test, and the SAMPLE=TWO option specifies a two-sample test. For a two-sample test, the WEIGHT= option specifies the sample size allocation weights for the two groups.
Input Number of Events for Fixed-Sample Design
The MODEL=INPUTNOBS option derives the number of events required for a group sequential trial from the number of events 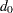 for the corresponding fixed-sample design. With the D=
for the corresponding fixed-sample design. With the D= 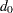 option specifies the number of events
option specifies the number of events 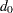 for a fixed-sample survival analysis, the number of events required for a group sequential trial is then computed as
for a fixed-sample survival analysis, the number of events required for a group sequential trial is then computed as
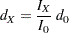 |
where 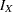 is the maximum information for the group sequential design and
is the maximum information for the group sequential design and 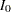 is the information for the corresponding fixed-sample design. The information ratio between
is the information for the corresponding fixed-sample design. The information ratio between 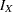 and
and 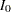 is derived in the SEQDESIGN procedure.
is derived in the SEQDESIGN procedure.
The SAMPLE=ONE option specifies a one-sample test, and the SAMPLE=TWO option specifies a two-sample test. For a two-sample test, the WEIGHT= option specifies the sample size allocation weights for the two groups.
With the computed number of events 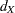 for a group sequential survival design, the required total sample size and sample size at each stage can be derived with specifications of hazard rates, accrual rate, and accrual time.
for a group sequential survival design, the required total sample size and sample size at each stage can be derived with specifications of hazard rates, accrual rate, and accrual time.
For a study group, if the hazard rate 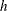 is constant, corresponding to an exponential survival distribution, and the individual accrual is uniform in the accrual time
is constant, corresponding to an exponential survival distribution, and the individual accrual is uniform in the accrual time 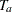 with a constant accrual rate
with a constant accrual rate 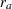 , Kim and Tsiatis (1990, pp. 83–84) show that the expected number of events by time
, Kim and Tsiatis (1990, pp. 83–84) show that the expected number of events by time  is given by
is given by
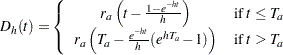 |
For a one-sample design, such as a proportional hazards regression, the expected number of events by time  is
is 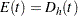 , where
, where 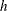 is the hazard rate for the group. For a two-sample design, such as a log-rank test for two survival distributions, the expected number of events by time
is the hazard rate for the group. For a two-sample design, such as a log-rank test for two survival distributions, the expected number of events by time  is
is
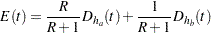 |
where 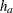 and
and 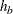 are hazard rates in groups A and B, respectively, and
are hazard rates in groups A and B, respectively, and 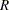 is the ratio of the sample size allocation weights
is the ratio of the sample size allocation weights 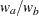 .
.
If the accrual rate 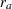 is specified without the accrual time
is specified without the accrual time 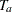 , follow-up time
, follow-up time 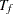 , and total study time
, and total study time 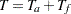 , the SEQDESIGN procedure computes the minimum and maximum accrual times from the following equation, as described in Kim and Tsiatis (1990, p. 85):
, the SEQDESIGN procedure computes the minimum and maximum accrual times from the following equation, as described in Kim and Tsiatis (1990, p. 85):
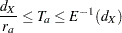 |
If the accrual rate 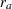 is specified with one of the three time parameters—the accrual time, follow-up time, and total study time—then the other two time parameters are computed in the SEQDESIGN procedure. Similarly, if the accrual rate
is specified with one of the three time parameters—the accrual time, follow-up time, and total study time—then the other two time parameters are computed in the SEQDESIGN procedure. Similarly, if the accrual rate 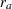 is not specified, but two of the three time parameters are specified, then the accrual rate is derived in the SEQDESIGN procedure.
is not specified, but two of the three time parameters are specified, then the accrual rate is derived in the SEQDESIGN procedure.
With the accrual rate 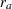 and the accrual time
and the accrual time 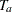 , the total sample size is
, the total sample size is
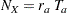 |
At each stage 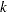 , the number of events is given by
, the number of events is given by
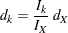 |
The corresponding time 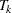 can be derived from the equation for the expected number of events,
can be derived from the equation for the expected number of events, 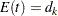 , and the resulting sample size is computed as
, and the resulting sample size is computed as
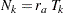 |
The following three sections describe examples of test statistics with their resulting information levels, which can then be used to derive the required sample size. The maximum likelihood estimators are used for all tests except to compare two survival distributions with a log-rank test, where a score statistic is used.