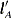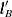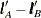The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement
PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement -
Details
 Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics
Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement
Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement - References
Example 53.16 Using the LSMEANS Statement
Recall the main-effects model fit to the Neuralgia data set in Example 53.2. The Treatment*Sex interaction, which was previously shown to be nonsignificant, is added back into the model for this discussion.
In the following statements, the ODDSRATIO statement is specified to produce odds ratios of pairwise differences of the Treatment parameters in the presence of the Sex interaction. The LSMEANS statement is specified with several options: the E option displays the coefficients that are used to compute the LS-means for each Treatment level, the DIFF option takes all pairwise differences of the LS-means for the levels of the Treatment variable, the ODDSRATIO option computes odds ratios of these differences, the CL option produces confidence intervals for the differences and odds ratios, and the ADJUST=BON option performs a very conservative adjustment of the p-values and confidence intervals.
proc logistic data=Neuralgia; class Treatment Sex / param=glm; model Pain= Treatment|Sex Age; oddsratio Treatment; lsmeans Treatment / e diff oddsratio cl adjust=bon; run;
The results from the ODDSRATIO statement are displayed in Output 53.16.1. All pairwise differences of levels of the Treatment effect are compared. However, because of the interaction between the Treatment and Sex variables, each difference is computed at each of the two levels of the Sex variable. These results show that the difference between Treatment levels A and B is insignificant for both genders.
To compute these odds ratios, you must first construct a linear combination of the parameters,  , for each level that is compared with all other levels fixed at some value. For example, to compare Treatment=A with B for Sex=F, you fix the Age variable at its mean, 70.05, and construct the following
, for each level that is compared with all other levels fixed at some value. For example, to compare Treatment=A with B for Sex=F, you fix the Age variable at its mean, 70.05, and construct the following  vectors:
vectors:
Treatment |
Sex |
Treatment*Sex |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Intercept |
A |
B |
P |
F |
M |
AF |
AM |
BF |
BM |
PF |
PM |
Age |
|||
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
70.05 |
||
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
70.05 |
||
|
0 |
1 |
–1 |
0 |
0 |
0 |
1 |
0 |
–1 |
0 |
0 |
0 |
0 |
||
Then the odds ratio for Treatment A versus B at Sex=F is computed as 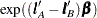 . Different
. Different  vectors must be similarly constructed when Sex=M because the resulting odds ratio will be different due to the interaction.
vectors must be similarly constructed when Sex=M because the resulting odds ratio will be different due to the interaction.
| Odds Ratio Estimates and Wald Confidence Intervals | |||
|---|---|---|---|
| Label | Estimate | 95% Confidence Limits | |
| Treatment A vs B at Sex=F | 0.398 | 0.016 | 9.722 |
| Treatment A vs P at Sex=F | 16.892 | 1.269 | 224.838 |
| Treatment B vs P at Sex=F | 42.492 | 2.276 | 793.254 |
| Treatment A vs B at Sex=M | 0.663 | 0.078 | 5.623 |
| Treatment A vs P at Sex=M | 34.766 | 1.807 | 668.724 |
| Treatment B vs P at Sex=M | 52.458 | 2.258 | >999.999 |
The results from the LSMEANS statement are displayed in Output 53.16.2 through Output 53.16.4.
The LS-means are computed by constructing each of the  coefficient vectors shown in Output 53.16.2, and then computing
coefficient vectors shown in Output 53.16.2, and then computing  . The LS-means are not estimates of the event probabilities; they are estimates of the linear predictors on the logit scale. In order to obtain event probabilities, you need to apply the inverse-link transformation by specifying the ILINK option in the LSMEANS statement. Notice in Output 53.16.2 that the Sex rows do not indicate either Sex=F or Sex=M. Instead, the LS-means are computed at an average of these two levels, so only one result needs to be reported. For more information about the construction of LS-means, see the section Construction of Least Squares Means of
Chapter 41,
The GLM Procedure.
. The LS-means are not estimates of the event probabilities; they are estimates of the linear predictors on the logit scale. In order to obtain event probabilities, you need to apply the inverse-link transformation by specifying the ILINK option in the LSMEANS statement. Notice in Output 53.16.2 that the Sex rows do not indicate either Sex=F or Sex=M. Instead, the LS-means are computed at an average of these two levels, so only one result needs to be reported. For more information about the construction of LS-means, see the section Construction of Least Squares Means of
Chapter 41,
The GLM Procedure.
| Coefficients for Treatment Least Squares Means | |||||
|---|---|---|---|---|---|
| Parameter | Treatment | Sex | Row1 | Row2 | Row3 |
| Intercept: Pain=No | 1 | 1 | 1 | ||
| Treatment A | A | 1 | |||
| Treatment B | B | 1 | |||
| Treatment P | P | 1 | |||
| Sex F | F | 0.5 | 0.5 | 0.5 | |
| Sex M | M | 0.5 | 0.5 | 0.5 | |
| Treatment A * Sex F | A | F | 0.5 | ||
| Treatment A * Sex M | A | M | 0.5 | ||
| Treatment B * Sex F | B | F | 0.5 | ||
| Treatment B * Sex M | B | M | 0.5 | ||
| Treatment P * Sex F | P | F | 0.5 | ||
| Treatment P * Sex M | P | M | 0.5 | ||
| Age | 70.05 | 70.05 | 70.05 | ||
The Treatment LS-means shown in Output 53.16.3 are all significantly nonzero at the 0.05 level. These LS-means are predicted population margins of the logits; that is, they estimate the marginal means over a balanced population, and they are effectively the within-Treatment means appropriately adjusted for the other effects in the model. The LS-means are not event probabilities; in order to obtain event probabilities, you need to apply the inverse-link transformation by specifying the ILINK option in the LSMEANS statement. For more information about LS-means, see the section LSMEANS Statement of Chapter 19, Shared Concepts and Topics.
| Treatment Least Squares Means | |||||||
|---|---|---|---|---|---|---|---|
| Treatment | Estimate | Standard Error | z Value | Pr > |z| | Alpha | Lower | Upper |
| A | 1.3195 | 0.6664 | 1.98 | 0.0477 | 0.05 | 0.01331 | 2.6257 |
| B | 1.9864 | 0.7874 | 2.52 | 0.0116 | 0.05 | 0.4431 | 3.5297 |
| P | -1.8682 | 0.7620 | -2.45 | 0.0142 | 0.05 | -3.3618 | -0.3747 |
Pairwise differences between the Treatment LS-means, requested with the DIFF option, are displayed in Output 53.16.4. The LS-mean for the level that is displayed in the _Treatment column is subtracted from the LS-mean for the level in the Treatment column, so the first row displays the LS-mean for Treatment level A minus the LS-mean for Treatment level B. The Pr > |z| column indicates that the A and B levels are not significantly different; however, both of these levels are different from level P. If the inverse-link transformation is specified with the ILINK option, then these differences do not transform back to differences in probabilities.
There are two odds ratios for Treatment level A versus B in Output 53.16.1; these are constructed at each level of the interacting covariate Sex. In contrast, there is only one LS-means odds ratio for Treatment level A versus B in Output 53.16.4. This odds ratio is computed at an average of the interacting effects by creating the  vectors shown in Output 53.16.2 (the Row1 column corresponds to
vectors shown in Output 53.16.2 (the Row1 column corresponds to  and the Row2 column corresponds to
and the Row2 column corresponds to 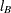 ) and computing
) and computing 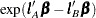 .
.
Since multiple tests are performed, you can protect yourself from falsely significant results by adjusting your p-values for multiplicity. The ADJUST=BON option performs the very conservative Bonferroni adjustment, and adds the columns labeled with 'Adj' to Output 53.16.4. Comparing the Pr > |z| column to the Adj P column, you can see that the p-values are adjusted upwards; in this case, there is no change in your conclusions. The confidence intervals are also adjusted for multiplicity—all adjusted intervals are wider than the unadjusted intervals, but again your conclusions in this example are unchanged.
| Differences of Treatment Least Squares Means Adjustment for Multiple Comparisons: Bonferroni |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Treatment | _Treatment | Estimate | Standard Error | z Value | Pr > |z| | Adj P | Alpha | Lower | Upper | Adj Lower | Adj Upper | Odds Ratio | Lower Confidence Limit for Odds Ratio |
Upper Confidence Limit for Odds Ratio |
Adj Lower Odds Ratio |
Adj Upper Odds Ratio |
| A | B | -0.6669 | 1.0026 | -0.67 | 0.5059 | 1.0000 | 0.05 | -2.6321 | 1.2982 | -3.0672 | 1.7334 | 0.513 | 0.072 | 3.663 | 0.047 | 5.660 |
| A | P | 3.1877 | 1.0376 | 3.07 | 0.0021 | 0.0064 | 0.05 | 1.1541 | 5.2214 | 0.7037 | 5.6717 | 24.234 | 3.171 | 185.195 | 2.021 | 290.542 |
| B | P | 3.8547 | 1.2126 | 3.18 | 0.0015 | 0.0044 | 0.05 | 1.4780 | 6.2313 | 0.9517 | 6.7576 | 47.213 | 4.384 | 508.441 | 2.590 | 860.612 |
If you want to jointly test whether the active treatments are different from the placebo, you can specify a custom hypothesis test with the LSMESTIMATE statement. In the following statements, the LS-means for the two treatments are contrasted against the LS-mean of the placebo, and the JOINT option performs a joint test that the two treatments are not different from placebo.
proc logistic data=Neuralgia; class Treatment Sex / param=glm; model Pain= Treatment|Sex Age; lsmestimate treatment 1 0 -1, 0 1 -1 / joint; run;
Output 53.16.5 displays the results from the LSMESTIMATE statement. The "Least Squares Means Estimate" table displays the differences of the two active treatments against the placebo, and the results are identical to the second and third rows of Output 53.16.3. The "Chi-Square Test for Least Squares Means Estimates" table displays the joint test. In all of these tests, you reject the null hypothesis that the treatment has the same effect as the placebo.
| Least Squares Means Estimates | |||||
|---|---|---|---|---|---|
| Effect | Label | Estimate | Standard Error | z Value | Pr > |z| |
| Treatment | Row 1 | 3.1877 | 1.0376 | 3.07 | 0.0021 |
| Treatment | Row 2 | 3.8547 | 1.2126 | 3.18 | 0.0015 |
| Chi-Square Test for Least Squares Means Estimates |
|||
|---|---|---|---|
| Effect | Num DF | Chi-Square | Pr > ChiSq |
| Treatment | 2 | 12.13 | 0.0023 |
If you want to work with LS-means but you prefer to compute the Treatment odds ratios within the Sex levels in the same fashion as the ODDSRATIO statement does, you can specify the SLICE statement. In the following statements, you specify the same options in the SLICE statement as you do in the LSMEANS statement, except that you also specify the SLICEBY= option to perform an LS-means analysis partitioned into sets that are defined by the Sex variable:
proc logistic data=Neuralgia; class Treatment Sex / param=glm; model Pain= Treatment|Sex Age; slice Treatment*Sex / sliceby=Sex diff oddsratio cl adjust=bon; run;
The results for Sex=F are displayed in Output 53.16.6 and Output 53.16.7. The joint test in Output 53.16.6 tests the equality of the LS-means of the levels of Treatment for Sex=F, and rejects equality at level 0.05. In Output 53.16.7, the odds ratios and confidence intervals match those reported for Sex=F in Output 53.16.1, and multiplicity adjustments are performed.
| Chi-Square Test for Treatment*Sex Least Squares Means Slice |
|||
|---|---|---|---|
| Slice | Num DF | Chi-Square | Pr > ChiSq |
| Sex F | 2 | 8.22 | 0.0164 |
| Simple Differences of Treatment*Sex Least Squares Means Adjustment for Multiple Comparisons: Bonferroni |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slice | Treatment | _Treatment | Estimate | Standard Error | z Value | Pr > |z| | Adj P | Alpha | Lower | Upper | Adj Lower | Adj Upper | Odds Ratio | Lower Confidence Limit for Odds Ratio |
Upper Confidence Limit for Odds Ratio |
Adj Lower Odds Ratio |
Adj Upper Odds Ratio |
| Sex F | A | B | -0.9224 | 1.6311 | -0.57 | 0.5717 | 1.0000 | 0.05 | -4.1193 | 2.2744 | -4.8272 | 2.9824 | 0.398 | 0.016 | 9.722 | 0.008 | 19.734 |
| Sex F | A | P | 2.8269 | 1.3207 | 2.14 | 0.0323 | 0.0970 | 0.05 | 0.2384 | 5.4154 | -0.3348 | 5.9886 | 16.892 | 1.269 | 224.838 | 0.715 | 398.848 |
| Sex F | B | P | 3.7493 | 1.4933 | 2.51 | 0.0120 | 0.0361 | 0.05 | 0.8225 | 6.6761 | 0.1744 | 7.3243 | 42.492 | 2.276 | 793.254 | 1.190 | >999.999 |
Similarly, the results for Sex=M are shown in Output 53.16.8 and Output 53.16.9.
| Chi-Square Test for Treatment*Sex Least Squares Means Slice |
|||
|---|---|---|---|
| Slice | Num DF | Chi-Square | Pr > ChiSq |
| Sex M | 2 | 6.64 | 0.0361 |
| Simple Differences of Treatment*Sex Least Squares Means Adjustment for Multiple Comparisons: Bonferroni |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slice | Treatment | _Treatment | Estimate | Standard Error | z Value | Pr > |z| | Adj P | Alpha | Lower | Upper | Adj Lower | Adj Upper | Odds Ratio | Lower Confidence Limit for Odds Ratio |
Upper Confidence Limit for Odds Ratio |
Adj Lower Odds Ratio |
Adj Upper Odds Ratio |
| Sex M | A | B | -0.4114 | 1.0910 | -0.38 | 0.7061 | 1.0000 | 0.05 | -2.5496 | 1.7268 | -3.0231 | 2.2003 | 0.663 | 0.078 | 5.623 | 0.049 | 9.028 |
| Sex M | A | P | 3.5486 | 1.5086 | 2.35 | 0.0187 | 0.0560 | 0.05 | 0.5919 | 6.5054 | -0.06286 | 7.1601 | 34.766 | 1.807 | 668.724 | 0.939 | >999.999 |
| Sex M | B | P | 3.9600 | 1.6049 | 2.47 | 0.0136 | 0.0408 | 0.05 | 0.8145 | 7.1055 | 0.1180 | 7.8021 | 52.458 | 2.258 | >999.999 | 1.125 | >999.999 |