The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement
PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement -
Details
 Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics
Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement
Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement - References
Example 53.11 Conditional Logistic Regression for Matched Pairs Data
In matched pairs, or case-control, studies, conditional logistic regression is used to investigate the relationship between an outcome of being an event (case) or a nonevent (control) and a set of prognostic factors.
The following data are a subset of the data from the Los Angeles Study of the Endometrial Cancer Data in Breslow and Day (1980). There are 63 matched pairs, each consisting of a case of endometrial cancer (Outcome=1) and a control (Outcome=0). The case and corresponding control have the same ID. Two prognostic factors are included: Gall (an indicator variable for gall bladder disease) and Hyper (an indicator variable for hypertension). The goal of the case-control analysis is to determine the relative risk for gall bladder disease, controlling for the effect of hypertension.
data Data1;
do ID=1 to 63;
do Outcome = 1 to 0 by -1;
input Gall Hyper @@;
output;
end;
end;
datalines;
0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1
0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 1 1 0 0 1 1 0 1 0 1 0 0 1
0 1 0 0 0 0 1 1 0 0 1 1 0 0 0 1 0 1 0 0
0 0 1 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0
0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 1 1 1
0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 0
0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0
0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1
0 0 0 0 0 1 0 1 0 1 0 0 0 1 0 0 1 0 0 0
0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0
1 0 1 0 0 1 0 0 1 0 0 0
;
There are several ways to approach this problem with PROC LOGISTIC:
Specify the STRATA statement to perform a conditional logistic regression.
Specify EXACT and STRATA statements to perform an exact logistic regression on the original data set, if you believe the data set is too small or too sparse for the usual asymptotics to hold.
Transform each matched pair into a single observation, and then specify a PROC LOGISTIC statement on this transformed data without a STRATA statement; this also performs a conditional logistic regression and produces essentially the same results.
Specify an EXACT statement on the transformed data.
SAS statements and selected results for these four approaches are given in the remainder of this example.
Conditional Analysis Using the STRATA Statement
In the following statements, PROC LOGISTIC is invoked with the ID variable declared in the STRATA statement to obtain the conditional logistic model estimates for a model containing Gall as the only predictor variable:
proc logistic data=Data1; strata ID; model outcome(event='1')=Gall; run;
Results from the conditional logistic analysis are shown in Output 53.11.1. Note that there is no intercept term in the "Analysis of Maximum Likelihood Estimates" tables.
The odds ratio estimate for Gall is 2.60, which is marginally significant (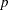 =0.0694) and which is an estimate of the relative risk for gall bladder disease. A 95% confidence interval for this relative risk is (0.927, 7.293).
=0.0694) and which is an estimate of the relative risk for gall bladder disease. A 95% confidence interval for this relative risk is (0.927, 7.293).
| Model Information | |
|---|---|
| Data Set | WORK.DATA1 |
| Response Variable | Outcome |
| Number of Response Levels | 2 |
| Number of Strata | 63 |
| Model | binary logit |
| Optimization Technique | Newton-Raphson ridge |
| Number of Observations Read | 126 |
|---|---|
| Number of Observations Used | 126 |
| Response Profile | ||
|---|---|---|
| Ordered Value |
Outcome | Total Frequency |
| 1 | 0 | 63 |
| 2 | 1 | 63 |
| Strata Summary | ||||
|---|---|---|---|---|
| Response Pattern |
Outcome | Number of Strata |
Frequency | |
| 0 | 1 | |||
| 1 | 1 | 1 | 63 | 126 |
| Convergence criterion (GCONV=1E-8) satisfied. |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Without Covariates |
With Covariates |
| AIC | 87.337 | 85.654 |
| SC | 87.337 | 88.490 |
| -2 Log L | 87.337 | 83.654 |
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 3.6830 | 1 | 0.0550 |
| Score | 3.5556 | 1 | 0.0593 |
| Wald | 3.2970 | 1 | 0.0694 |
| Analysis of Maximum Likelihood Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq |
| Gall | 1 | 0.9555 | 0.5262 | 3.2970 | 0.0694 |
| Odds Ratio Estimates | |||
|---|---|---|---|
| Effect | Point Estimate | 95% Wald Confidence Limits |
|
| Gall | 2.600 | 0.927 | 7.293 |
Exact Analysis Using the STRATA Statement
When you believe there are not enough data or that the data are too sparse, you can perform a stratified exact logistic regression. The following statements perform stratified exact logistic regressions on the original data set by specifying both the STRATA and EXACT statements:
proc logistic data=Data1 exactonly; strata ID; model outcome(event='1')=Gall; exact Gall / estimate=both; run;
| Conditional Exact Tests | ||||
|---|---|---|---|---|
| Effect | Test | Statistic | p-Value | |
| Exact | Mid | |||
| Gall | Score | 3.5556 | 0.0963 | 0.0799 |
| Probability | 0.0327 | 0.0963 | 0.0799 | |
| Exact Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error | 95% Confidence Limits | Two-sided p-Value | |
| Gall | 0.9555 | 0.5262 | -0.1394 | 2.2316 | 0.0963 |
| Exact Odds Ratios | ||||
|---|---|---|---|---|
| Parameter | Estimate | 95% Confidence Limits | Two-sided p-Value | |
| Gall | 2.600 | 0.870 | 9.315 | 0.0963 |
Note that the score statistic in the "Conditional Exact Tests" table in Output 53.11.2 is identical to the score statistic in Output 53.11.1 from the conditional analysis. The exact odds ratio confidence interval is much wider than its conditional analysis counterpart, but the parameter estimates are similar. The exact analysis confirms the marginal significance of Gall as a predictor variable.
Conditional Analysis Using Transformed Data
When each matched set consists of one event and one nonevent, the conditional likelihood is given by
 |
where  and
and  are vectors representing the prognostic factors for the event and nonevent, respectively, of the
are vectors representing the prognostic factors for the event and nonevent, respectively, of the 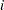 th matched set. This likelihood is identical to the likelihood of fitting a logistic regression model to a set of data with constant response, where the model contains no intercept term and has explanatory variables given by
th matched set. This likelihood is identical to the likelihood of fitting a logistic regression model to a set of data with constant response, where the model contains no intercept term and has explanatory variables given by  (Breslow; 1982).
(Breslow; 1982).
To apply this method, the following DATA step transforms each matched pair into a single observation, where the variables Gall and Hyper contain the differences between the corresponding values for the case and the control (case–control). The variable Outcome, which will be used as the response variable in the logistic regression model, is given a constant value of 0 (which is the Outcome value for the control, although any constant, numeric or character, will suffice).
data Data2;
set Data1;
drop id1 gall1 hyper1;
retain id1 gall1 hyper1 0;
if (ID = id1) then do;
Gall=gall1-Gall; Hyper=hyper1-Hyper;
output;
end;
else do;
id1=ID; gall1=Gall; hyper1=Hyper;
end;
run;
Note that there are 63 observations in the data set, one for each matched pair. Since the number of observations  is halved, statistics that depend on
is halved, statistics that depend on  such as
such as 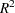 (see the Generalized Coefficient of Determination section) will be incorrect. The variable Outcome has a constant value of 0.
(see the Generalized Coefficient of Determination section) will be incorrect. The variable Outcome has a constant value of 0.
In the following statements, PROC LOGISTIC is invoked with the NOINT option to obtain the conditional logistic model estimates. Because the option CLODDS=PL is specified, PROC LOGISTIC computes a 95% profile-likelihood confidence interval for the odds ratio for each predictor variable; note that profile-likelihood confidence intervals are not currently available when a STRATA statement is specified.
proc logistic data=Data2; model outcome=Gall / noint clodds=PL; run;
The results are not displayed here.
Exact Analysis Using Transformed Data
Sometimes the original data set in a matched-pairs study is too large for the exact methods to handle. In such cases it might be possible to use the transformed data set. The following statements perform exact logistic regressions on the transformed data set. The results are not displayed here.
proc logistic data=Data2 exactonly; model outcome=Gall / noint; exact Gall / estimate=both; run;