The LOGISTIC Procedure

OUTEST= Output Data Set

The OUTEST= data set contains one observation for each BY group containing the maximum likelihood estimates of the regression coefficients. If you also use the COVOUT option in the PROC LOGISTIC statement, there are additional observations containing the rows of the estimated covariance matrix. If you specify SELECTION=FORWARD, BACKWARD, or STEPWISE, only the estimates of the parameters and covariance matrix for the final model are output to the OUTEST= data set.

proc logistic;
   class Gender;
   model Net3 = Age Gender / link=glogit;
run;

INEST= Input Data Set

You can specify starting values for the iterative algorithm in the INEST= data set. The INEST= data set has the same structure as the OUTEST= data set but is not required to have all the variables or observations that appear in the OUTEST= data set. A previous OUTEST= data set can be used as, or modified for use as, an INEST= data set.

The INEST= data set must contain the intercept variables (named Intercept for binary response models and Intercept, Intercept_2, Intercept_3, and so forth, for ordinal and nominal response models) and all explanatory variables in the MODEL statement. If BY processing is used, the INEST= data set should also include the BY variables, and there must be one observation for each BY group. If the INEST= data set also contains the _TYPE_ variable, only observations with _TYPE_ value ’PARMS’ are used as starting values.

OUT= Output Data Set in the OUTPUT Statement

The OUT= data set in the OUTPUT statement contains all the variables in the input data set along with statistics you request by specifying keyword=name options or the PREDPROBS= option in the OUTPUT statement. In addition, if you use the single-trial syntax and you request any of the XBETA=, STDXBETA=, PREDICTED=, LCL=, and UCL= options, the OUT= data set contains the automatic variable _LEVEL_. The value of _LEVEL_ identifies the response category upon which the computed values of XBETA=, STDXBETA=, PREDICTED=, LCL=, and UCL= are based.

When there are more than two response levels, only variables named by the XBETA=, STDXBETA=, PREDICTED=, LOWER=, and UPPER= options and the variables given by PREDPROBS=(INDIVIDUAL CUMULATIVE) have their values computed; the other variables have missing values. If you fit a generalized logit model, the cumulative predicted probabilities are not computed.

When there are only two response categories, each input observation produces one observation in the OUT= data set.

If there are more than two response categories and you specify only the PREDPROBS= option, then each input observation produces one observation in the OUT= data set. However, if you fit an ordinal (cumulative) model and specify options other than the PREDPROBS= options, each input observation generates as many output observations as one fewer than the number of response levels, and the predicted probabilities and their confidence limits correspond to the cumulative predicted probabilities. If you fit a generalized logit model and specify options other than the PREDPROBS= options, each input observation generates as many output observations as the number of response categories; the predicted probabilities and their confidence limits correspond to the probabilities of individual response categories.

For observations in which only the response variable is missing, values of the XBETA=, STDXBETA=, PREDICTED=, UPPER=, LOWER=, and the PREDPROBS= options are computed even though these observations do not affect the model fit. This enables, for instance, predicted probabilities to be computed for new observations.

OUT= Output Data Set in a SCORE Statement

The OUT= data set in a SCORE statement contains all the variables in the data set being scored. The data set being scored can be either the input DATA= data set in the PROC LOGISTIC statement or the DATA= data set in the SCORE statement. The DATA= data set in the SCORE statement does not need to contain the response variable.

If the data set being scored contains the response variable, then denote the normalized levels (left-justified, formatted values of 16 characters or less) of your response variable Y by 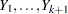. For each response level, the OUT= data set also contains the following:

• F_Y, the normalized levels of the response variable Y in the data set being scored. If the events/trials syntax is used, the F_Y variable is not created.

• I_Y, the normalized levels that the observations are classified into. Note that an observation is classified into the level with the largest probability. If the events/trials syntax is used, the _INTO_ variable is created instead, and it contains the values EVENT and NONEVENT.

• P_Y, the posterior probabilities of the normalized response level Y

• If the CLM option is specified in the SCORE statement, the OUT= data set also includes the following:

  • LCL_Y, the lower 100()% confidence limits for P_Y

  • UCL_Y, the upper 100()% confidence limits for P_Y

OUTDIST= Output Data Set

The OUTDIST= data set contains every exact conditional distribution necessary to process the corresponding EXACT statement. For example, the following statements create one distribution for the x1 parameter and another for the x2 parameters, and produce the data set dist shown in Table 53.10:

data test;
   input y x1 x2 count;
   datalines;
0 0 0 1
1 0 0 1
0 1 1 2
1 1 1 1
1 0 2 3
1 1 2 1
1 2 0 3
1 2 1 2
1 2 2 1
;

proc logistic data=test exactonly;
   class x2 / param=ref;
   model y=x1 x2;
   exact x1 x2/ outdist=dist;
proc print data=dist; 
run;

The first nine observations in the dist data set contain an exact distribution for the parameters of the x2 effect (hence the values for the x1 parameter are missing), and the remaining five observations are for the x1 parameter. If a joint distribution was created, there would be observations with values for both the x1 and x2 parameters. For CLASS variables, the corresponding parameters in the dist data set are identified by concatenating the variable name with the appropriate classification level.

The data set contains the possible sufficient statistics of the parameters for the effects specified in the EXACT statement, and the Count variable contains the number of different responses that yield these statistics. In particular, there are six possible response vectors 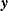for which the dot product 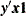was equal to 2, and for which 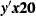, , 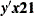and were equal to their actual observed values (displayed in the "Sufficient Statistics" table).

When hypothesis tests are performed on the parameters, the Prob variable contains the probability of obtaining that statistic (which is just the count divided by the total count), and the Score variable contains the score for that statistic.

The OUTDIST= data set can contain a different exact conditional distribution for each specified EXACT statement. For example, consider the following EXACT statements:

exact 'O1'   x1    /           outdist=o1;
exact 'OJ12' x1 x2 / jointonly outdist=oj12;
exact 'OA12' x1 x2 / joint     outdist=oa12;
exact 'OE12' x1 x2 / estimate  outdist=oe12;

The O1 statement outputs a single exact conditional distribution. The OJ12 statement outputs only the joint distribution for x1 and x2. The OA12 statement outputs three conditional distributions: one for x1, one for x2, and one jointly for x1 and x2. The OE12 statement outputs two conditional distributions: one for x1 and the other for x2. Data set oe12 contains both the x1 and x2 variables; the distribution for x1 has missing values in the x2 column while the distribution for x2 has missing values in the x1 column.

OUTROC= Output Data Set

The OUTROC= data set contains data necessary for producing the ROC curve, and can be created by specifying the OUTROC= option in the MODEL statement or the OUTROC= option in the SCORE statement: It has the following variables:

• any BY variables specified

• _STEP_, the model step number. This variable is not included if model selection is not requested.

• _PROB_, the estimated probability of an event. These estimated probabilities serve as cutpoints for predicting the response. Any observation with an estimated event probability that exceeds or equals _PROB_ is predicted to be an event; otherwise, it is predicted to be a nonevent. Predicted probabilities that are close to each other are grouped together, with the maximum allowable difference between the largest and smallest values less than a constant that is specified by the ROCEPS= option. The smallest estimated probability is used to represent the group.

• _POS_, the number of correctly predicted event responses

• _NEG_, the number of correctly predicted nonevent responses

• _FALPOS_, the number of falsely predicted event responses

• _FALNEG_, the number of falsely predicted nonevent responses

• _SENSIT_, the sensitivity, which is the proportion of event observations that were predicted to have an event response

• _1MSPEC_, one minus specificity, which is the proportion of nonevent observations that were predicted to have an event response

Note that none of these statistics are affected by the bias-correction method discussed in the section Classification Table. An ROC curve is obtained by plotting _SENSIT_ against _1MSPEC_.

For more information, see the section Receiver Operating Characteristic Curves.