The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement -
Details
Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics
-
Examples
Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement
- References
| ODDSRATIO Statement |
The ODDSRATIO statement produces odds ratios for variable even when the variable is involved in interactions with other covariates, and for classification variables that use any parameterization. You can also specify variables on which constructed effects are based, in addition to the names of COLLECTION or MULTIMEMBER effects. You can specify several ODDSRATIO statements.
If variable is continuous, then the odds ratios honor any values specified in the UNITS statement. If variable is a classification variable, then odds ratios comparing each pairwise difference between the levels of variable are produced. If variable interacts with a continuous variable, then the odds ratios are produced at the mean of the interacting covariate by default. If variable interacts with a classification variable, then the odds ratios are produced at each level of the interacting covariate by default. The computed odds ratios are independent of the parameterization of any classification variable.
The odds ratios are uniquely labeled by concatenating the following terms to variable:
If this is a polytomous response model, then prefix the response variable and the level describing the logit followed by a colon; for example, "Y 0:".
If variable is continuous and the UNITS statement provides a value that is not equal to 1, then append "Units=value"; otherwise, if variable is a classification variable, then append the levels being contrasted; for example, "cat vs dog".
Append all interacting covariates preceded by "At"; for example, "At X=1.2 A=cat".
If you are also creating odds ratio plots, then this label is displayed on the plots (see the PLOTS option for more information). If you specify a ’label’ in the ODDSRATIO statement, then the odds ratios produced by this statement are also labeled: ’label’, ’label 2’, ’label 3’,..., and these are the labels used in the plots. If there are any duplicated labels across all ODDSRATIO statements, then the corresponding odds ratios are not displayed on the plots.
The following options are available:
- AT(covariate=value-list | REF | ALL<...covariate=value-list | REF | ALL>)
-
specifies fixed levels of the interacting covariates. If a specified covariate does not interact with the variable, then its AT list is ignored.
For continuous interacting covariates, you can specify one or more numbers in the value-list. For classification covariates, you can specify one or more formatted levels of the covariate enclosed in single quotes (for example, A=’cat’ ’dog’), you can specify the keyword REF to select the reference-level, or you can specify the keyword ALL to select all levels of the classification variable. By default, continuous covariates are set to their means, while CLASS covariates are set to ALL. For a model that includes a classification variable A={cat,dog} and a continuous covariate X, specifying AT(A=’cat’ X=7 9) will set A to ’cat’, and X to
and then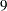 
. - CL=WALD | PL | BOTH
specifies whether to create Wald or profile-likelihood confidence limits, or both. By default, Wald confidence limits are produced.
- DIFF=REF | ALL
specifies whether the odds ratios for a classification variable are computed against the reference level, or all pairs of variable are compared. By default, DIFF=ALL. The DIFF= option is ignored when variable is continuous.
- PLCONV=value
controls the convergence criterion for confidence intervals based on the profile-likelihood function. The quantity value must be a positive number, with a default value of 1E–4. The PLCONV= option has no effect if profile-likelihood confidence intervals (CL=PL) are not requested.
- PLMAXITER=n
specifies the maximum number of iterations to perform. By default, PLMAXITER=25. If convergence is not attained in n iterations, the odds ratio or the confidence limits are set to missing. The PLMAXITER= option has no effect if profile-likelihood confidence intervals (CL=PL) are not requested.
- PLSINGULAR=value
specifies the tolerance for testing the singularity of the Hessian matrix (Newton-Raphson algorithm) or the expected value of the Hessian matrix (Fisher scoring algorithm). The test requires that a pivot for sweeping this matrix be at least this number times a norm of the matrix. Values of the PLSINGULAR= option must be numeric. By default, value is the machine epsilon times 1E7, which is approximately 1E–9. The PLSINGULAR= option has no effect if profile-likelihood confidence intervals (CL=PL) are not requested.