Previous Page | Next Page

LSMEANS Statement

This statement documentation applies to the following procedures:
GENMOD, LOGISTIC, ORTHOREG, PHREG, PLM, SURVEYLOGISTIC, SURVEYPHREG, and SURVEYREG.
The GLIMMIX, GLM, and MIXED procedures also support LSMEANS statements. The relevant statement documentation for these procedures can be found in the specific procedure chapter.

The LSMEANS statement computes least squares means (LS-means) of fixed effects. In the GLM, MIXED, and GLIMMIX procedures, LS-means are predicted population margins—that is, they estimate the marginal means over a balanced population. In a sense, LS-means are to unbalanced designs as class and subclass arithmetic means are to balanced designs.

Thus it is important not to interpret the name with a strict association with least squares estimation. Least squares is the predominant estimation technique for the type of models in which LS-means were first applied. Their interpretation and importance reaches beyond the least squares principle, however. A more appropriate approach to LS-means views them as linear combinations of the parameter estimates that are constructed in such a way that they correspond to average predicted values in a population where the levels of classification variables are balanced.

This contemporary—and historically correct—interpretation of the concept of least squares means underlines their importance in all classes of models where predicted values are reasonably formed as linear combinations of the parameter estimates. 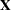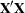LS-means distinguish themselves from general estimable functions in that they take the structure for the model and data into account through the structure of the $\text{[math]}$ and $\text{[math]}$ matrix in your model. For example, in a generalized linear model the structure of the 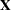$\text{[math]}$ matrix informs the analysis about the possible levels of classification variables and predictions on the linear (the linked) scale are computed as 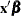$\text{[math]}$ . LS-means are thus meaningful quantities in such models when the linear estimable function that corresponds to an averaged prediction is constructed on the linked scale. For example, in a binomial model with logit link, the least squares means are predicted population margins of the logits. You can then transform the least squares means to the data scale with the ILINK option, and you can display differences of least squares means in terms of odds ratios with the ODDSRATIO option. The underlying principle—unless you perform a Bayesian analysis—is to construct the estimates or their differences on the linked scale and to apply appropriate transformations in a second step.

Least squares means computations are also supported for multinomial models.

LS-means are computed as 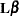$\text{[math]}$ where the 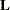$\text{[math]}$ matrix that is constructed to compute the predicted values is the same as the 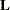$\text{[math]}$ matrix that is formed in PROC GLM.

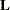Each LS-mean is computed as $\text{[math]}$ , where $\text{[math]}$ is the coefficient matrix that is associated with the least squares mean and 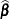$\text{[math]}$ is the estimate of the fixed-effects parameter vector. The approximate standard error for the LS-mean is computed as the square root of 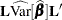$\text{[math]}$ . The approximate variance matrix of the fixed-effects estimates depends on the estimation method.