The QUANTSELECT Procedure

Quantile Regression

Subsections:

This section describes the basic concepts and notations for quantile regression and quantile regression model selection.

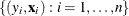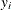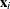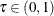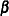Let $\{ (y_ i,\mb{x}_ i):i=1,\ldots ,n\} $ denote a data set of observations, where $y_ i$ are responses, and $\mb{x}_ i$ are regressors. Koenker and Bassett (1978) defined the regression quantile at quantile level $\tau \in (0,1)$ as any solution that minimizes the following objective function in $\bbeta $:

\[ \sum _{i=1}^ n \rho _\tau \left(y_ i-\mb{x}_ i^{\prime }\bbeta \right) \]

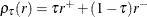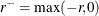where $\rho _\tau (r)=\tau r^+ +(1-\tau )r^-$ is a check loss function in which $r^+=\max (r,0)$ and $r^-=\max (-r,0)$.

If you specify weights 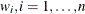$w_ i, i=1,\ldots ,n$, in the WEIGHT statement, weighted quantile regression is carried out by solving

\[ \min _{\bbeta \in \mb{R}^ p} \sum _{i=1}^ n \rho _\tau \left(w_ i(y_ i-\mb{x}_ i^{\prime }\bbeta )\right) \]