The QUANTSELECT Procedure
Example 96.1 Simulation Study
This simulation study exemplifies the unity of motive and effect for the PROC QUANTSELECT procedure. The following statements generate a data set that is based on a naive instrumental model (Chernozhukov and Hansen 2008):
%let seed=321;
%let p=20;
%let n=3000;
data analysisData;
array x{&p} x1-x&p;
do i=1 to &n;
U = ranuni(&seed);
x1 = ranuni(&seed);
x2 = ranexp(&seed);
x3 = abs(rannor(&seed));
y = x1*(U-0.1) + x2*(U*U-0.25) + x3*(exp(U)-exp(0.9));
do j=4 to &p;
x{j} = ranuni(&seed);
end;
output;
end;
run;
Variable U of the data set indicates the true quantile level of the response y conditional on 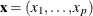 .
.
Let 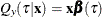 denote the underlying quantile regression model, where
denote the underlying quantile regression model, where 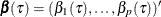 . Then, the true parameter functions are
. Then, the true parameter functions are
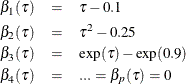
It is easy to see that, at 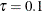 , only
, only 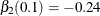 and
and 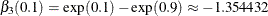 are nonzero parameters. Therefore, an effective effect selection method should select
are nonzero parameters. Therefore, an effective effect selection method should select  and
and 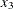 and drop all the other effects in this data set at
and drop all the other effects in this data set at 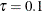 . By the same rationale,
. By the same rationale, 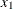 and
and 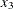 should be selected at
should be selected at 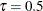 with
with 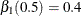 and
and 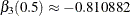 , and
, and 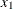 and
and 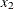 should be selected at
should be selected at 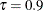 with
with 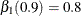 and
and 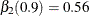 .
.
The following statements use PROC QUANTSELECT with the adaptive LASSO method:
proc quantselect data=analysisData;
model y= x1-x&p / quantile=0.1 0.5 0.9
selection=lasso(adaptive);
output out=out p=pred;
run;
Output 96.1.1 shows that, by default, the CHOOSE= and STOP= options are both set to SBC.
Output 96.1.1: Model Information
The selected effects and the relevant estimates are shown in Output 96.1.2 for 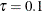 , Output 96.1.3 for
, Output 96.1.3 for 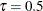 , and Output 96.1.4 for
, and Output 96.1.4 for 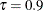 . You can see that the adaptive LASSO method correctly selects active effects for all three quantile levels.
. You can see that the adaptive LASSO method correctly selects active effects for all three quantile levels.
Output 96.1.2: Parameter Estimates at 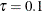
Output 96.1.3: Parameter Estimates at 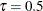
Output 96.1.4: Parameter Estimates at 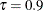
The QUANTSELECT procedure can perform effect selection not only at a single quantile level but also for the entire quantile
process. You can specify the QUANTILE=PROCESS option to do effect selection for the entire quantile process. With the QUANTILE=PROCESS
option specified, the ParameterEstimates table produced by the QUANTSELECT procedure actually shows the mean prediction model
of y conditional on  . In this simulation study, the true mean model is
. In this simulation study, the true mean model is
![\[ \mbox{E}(y|\mb{x})=\mb{x}\bbeta \]](images/statug_qrsel0183.png)
where
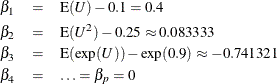
The following statements perform effect selection for the quantile process with the forward selection method.
proc quantselect data=analysisData;
model y= x1-x&p / quantile=process(ntau=all)
selection=forward;
run;
Output 96.1.5 shows that, by default, the SELECT= and STOP= options are both set to SBC. The selected effects and the relevant estimates for the conditional mean model are shown in Output 96.1.6.
Output 96.1.5: Model Information
Output 96.1.6: Parameter Estimates
Linear regression is the most popular method for estimating conditional means. The following statements show how to select effects with the GLMSELECT procedure, and Output 96.1.7 shows the resulting selected effects and their estimates. You can see that the mean estimates from the QUANTSELECT procedure are similar to those from the GLMSELECT procedure. However, quantile regression can provide detailed distribution information, which is not available from linear regression.
proc glmselect data=analysisData; model y= x1-x3 / selection=forward(select=sbc stop=sbc choose=sbc); run;
Output 96.1.7: Parameter Estimates
