The QUANTSELECT Procedure
Example 96.2 Econometric Growth Data
This example shows how you can use the QUANTREG procedure to further analyze the final selected models from the QUANTSELECT procedure, and how you can find the set of observations for a specified range of quantile levels. The data under investigation contain economic growth rate records for countries during two time periods: 1965–1975 and 1975–1985. This data set comes from a study by Barro and Lee (1994) and is also analyzed in the section Quantile Regression for Econometric Growth Data of Chapter 95: The QUANTREG Procedure.
The data set contains 161 observations and 16 variables. The variables, which are listed in Table 96.18, include the national GDP growth rates (GDPR), 14 covariates, and a name variable (Country) that identifies the countries in one of the two periods.
Table 96.18: Variables for Econometric Growth Data
|
|
The goal is to compare the effect of the covariates on GDPR at different quantile levels. The following statements perform
effect selection at three quantile levels ( ): 0.1, 0.5, and 0.9.
): 0.1, 0.5, and 0.9.
data growth;
length Country$ 22;
input Country GDPR lgdp2 mse2 fse2 fhe2 mhe2 lexp2 lintr2 gedy2
Iy2 gcony2 lblakp2 pol2 ttrad2 @@;
if(index(country,'75')) then period='65-75';
if(index(country,'85')) then period='75-85';
datalines;
Algeria75 .0415 7.330 .1320 .0670 .0050 .0220 3.880 .1138 .0382
.1898 .0601 .3823 .0833 .1001
Algeria85 .0244 7.745 .2760 .0740 .0070 .0370 3.978 -.107 .0437
.3057 .0850 .9386 .0000 .0657
Argentina75 .0187 8.220 .7850 .6200 .0740 .1660 4.181 .4060 .0221
.1505 .0596 .1924 .3575 -.011
Argentina85 -.014 8.407 .9360 .9020 .1320 .2030 4.211 .1914 .0243
... more lines ...
.0654 .1224 .9393 .7022 -.007
Zambia75 .0120 6.989 .3760 .1190 .0130 .0420 3.757 .4388 .0339
.3688 .2513 .3945 .0000 -.032
Zambia85 -.046 7.109 .4200 .2740 .0110 .0270 3.854 .8812 .0477
.1632 .2637 .6467 .0000 -.033
Zimbabwe75 .0320 6.860 .1450 .0170 .0080 .0450 3.833 .7156 .0337
.2276 .0246 .1997 .0000 -.040
Zimbabwe85 -.011 7.180 .2200 .0650 .0060 .0400 3.944 .9296 .0520
.1559 .0518 .7862 .7161 -.024
;
proc quantselect data=growth;
class period;
model GDPR = period lgdp2 mse2 fse2 fhe2 mhe2 lexp2
lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
/ quantile=0.1 0.5 0.9 selection=backward(choose=sbc sh=5);
run;
The SELECTION=BACKWARD option specifies the BACKWARD method as the effect selection method, and the CHOOSE=SBC option specifies
the Schwarz Bayesian information criterion for choosing the final selected effects. The estimates for the final selected effects
are shown in Output 96.2.1 for 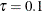 , Output 96.2.2 for
, Output 96.2.2 for 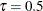 , and Output 96.2.3 for
, and Output 96.2.3 for 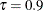 .
.
Output 96.2.1: Parameter Estimates at 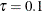
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | DF | Estimate | Standardized Estimate |
| Intercept | 1 | 0.048847 | 0 |
| period 65-75 | 1 | 0.011861 | 0.238272 |
| lgdp2 | 1 | -0.024613 | -0.947421 |
| mse2 | 1 | 0.016031 | 0.554367 |
| lexp2 | 1 | 0.033898 | 0.277298 |
| lintr2 | 1 | -0.001877 | -0.192986 |
| Iy2 | 1 | 0.067877 | 0.240002 |
| gcony2 | 1 | -0.176072 | -0.438350 |
| lblakp2 | 1 | -0.026364 | -0.326506 |
| pol2 | 1 | -0.022975 | -0.223264 |
| ttrad2 | 1 | 0.096604 | 0.146071 |
Output 96.2.2: Parameter Estimates at 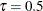
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | DF | Estimate | Standardized Estimate |
| Intercept | 1 | -0.040264 | 0 |
| period 65-75 | 1 | 0.008913 | 0.179063 |
| lgdp2 | 1 | -0.025823 | -0.993996 |
| mse2 | 1 | 0.014161 | 0.489697 |
| lexp2 | 1 | 0.062163 | 0.508527 |
| lintr2 | 1 | -0.002688 | -0.276345 |
| Iy2 | 1 | 0.068294 | 0.241476 |
| gcony2 | 1 | -0.096543 | -0.240354 |
| lblakp2 | 1 | -0.025265 | -0.312892 |
| pol2 | 1 | -0.019387 | -0.188396 |
| ttrad2 | 1 | 0.150668 | 0.227819 |
Output 96.2.3: Parameter Estimates at 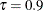
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | DF | Estimate | Standardized Estimate |
| Intercept | 1 | -0.011162 | 0 |
| lgdp2 | 1 | -0.032753 | -1.260735 |
| mse2 | 1 | 0.016583 | 0.573447 |
| lexp2 | 1 | 0.073326 | 0.599845 |
| lintr2 | 1 | -0.003334 | -0.342843 |
| Iy2 | 1 | 0.063929 | 0.226041 |
| gcony2 | 1 | -0.089998 | -0.224060 |
| lblakp2 | 1 | -0.032253 | -0.399439 |
| ttrad2 | 1 | 0.213457 | 0.322760 |
Comparing the three quantile models, you can see that the final selected models for 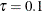 and
and 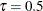 have the same set of selected effects, but the final selected model for
have the same set of selected effects, but the final selected model for 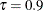 excludes the effects for time period and political instability. In other words, if a country’s annual change in per capita
GDP represents the 90% quantile conditional on the explanatory effects, then its GDP growth rate seems consistent for both
the 1965–1975 and 1975–1985 periods and resistant to political instability. In addition, if a country’s GDP growth rate represents
the 50% or less quantile conditional on the explanatory effects, then the country’s 1975–1985 GDP growth rate seems lower
than its 1965–1975 GDP growth rate, and the effect for political instability has a negative impact on its GDP growth rate.
excludes the effects for time period and political instability. In other words, if a country’s annual change in per capita
GDP represents the 90% quantile conditional on the explanatory effects, then its GDP growth rate seems consistent for both
the 1965–1975 and 1975–1985 periods and resistant to political instability. In addition, if a country’s GDP growth rate represents
the 50% or less quantile conditional on the explanatory effects, then the country’s 1975–1985 GDP growth rate seems lower
than its 1965–1975 GDP growth rate, and the effect for political instability has a negative impact on its GDP growth rate.
To further investigate the impact of time period and political instability on GDP growth rate, you can use the QUANTREG procedure
to test the final selected effects. In the previous statements, PROC QUANTSELECT creates a macro variable for the final selected
model at each of the three quantile levels. For the current example, the macro variable _QRSINDT1 contains the final model at 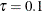 ;
; _QRSINDT2 contains the final model at 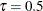 ; and
; and _QRSINDT3 contains the final model at 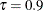 . The following statements show how to use
. The following statements show how to use _QRSINDT2 to specify the model for the QUANTREG procedure at 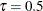 :
:
proc quantreg data=growth; class period; model GDPR = &_qrsindt2 / quantile=0.5; Time_Period: test period; Political_Instability: test pol2; run;
Output 96.2.4 shows more information for the final selected model at 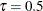 . Output 96.2.5 and Output 96.2.6 show the test results for the effects of time period and political instability on GDP growth rate. You can see that both
time period and political instability are significant for the
. Output 96.2.5 and Output 96.2.6 show the test results for the effects of time period and political instability on GDP growth rate. You can see that both
time period and political instability are significant for the 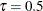 model.
model.
Output 96.2.4: Parameter Estimates at 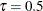
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | 95% Confidence Limits | ||
| Intercept | 1 | -0.0403 | -0.1529 | 0.0453 | |
| period | 65-75 | 1 | 0.0089 | 0.0060 | 0.0139 |
| period | 75-85 | 0 | 0.0000 | 0.0000 | 0.0000 |
| lgdp2 | 1 | -0.0258 | -0.0324 | -0.0212 | |
| mse2 | 1 | 0.0142 | 0.0068 | 0.0182 | |
| lexp2 | 1 | 0.0622 | 0.0400 | 0.1199 | |
| lintr2 | 1 | -0.0027 | -0.0045 | -0.0011 | |
| Iy2 | 1 | 0.0683 | 0.0143 | 0.1077 | |
| gcony2 | 1 | -0.0965 | -0.1526 | -0.0576 | |
| lblakp2 | 1 | -0.0253 | -0.0537 | -0.0174 | |
| pol2 | 1 | -0.0194 | -0.0377 | -0.0116 | |
| ttrad2 | 1 | 0.1507 | 0.0190 | 0.2436 | |
Output 96.2.5: Test Results at 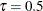
Output 96.2.6: Test Results at 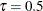
As mentioned earlier, _QRSINDT1 and _QRSINDT2 are identical, and _QRSINDT3 excludes two effects from _QRSINDT2: time period and political instability. The following statements retest time period and political instability for the final
selected model at 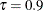 :
:
proc quantreg data=growth; class period; model GDPR = &_qrsindt2 / quantile=0.9; Time_Period: test period; Political_Instability: test pol2; Period_and_Political: test period pol2; run;
Output 96.2.7, Output 96.2.8, and Output 96.2.9 show the test results for the effects of time period and political instability on GDP growth rate at 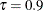 . You can see that time period, political instability, and their combination are all insignificant for the
. You can see that time period, political instability, and their combination are all insignificant for the 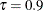 model.
model.
Output 96.2.7: Test Results at 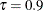
Output 96.2.8: Test Results at 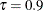
Output 96.2.9: Test Results at 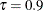
Another interesting question for quantile regression is to find the observations for a certain range of quantile levels. For
example, you might want to know which countries are winners in terms of conditional GDP growth rate at the 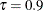 level. The following statements compute the
level. The following statements compute the 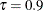 quantile predictions and then search, sort, and print the list of winner countries:
quantile predictions and then search, sort, and print the list of winner countries:
proc quantselect data=growth;
class period;
model GDPR = period lgdp2 mse2 fse2 fhe2 mhe2 lexp2
lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
/ quantile=0.9 selection=backward(choose=sbc sh=5);
output out=growth90Out p=Pred;
run;
data growth90;
set growth90Out;
drop lgdp2 mse2 fse2 fhe2 mhe2 lexp2 lintr2 gedy2 Iy2
gcony2 lblakp2 ttrad2;
where GDPR-Pred >= -1E-4;
GdpDiff = GDPR-Pred;
run;
proc sort data=growth90;
by GdpDiff;
run;
proc print data=growth90;
run;
Output 96.2.10 lists the countries whose conditional GDP growth rates are equal to or higher than their 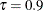 quantile predictions.
quantile predictions.
Output 96.2.10: Countries with High Conditional GDP Growth Rates at 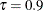 Level
Level
| Obs | Country | GDPR | pol2 | period | Pred | GdpDiff |
|---|---|---|---|---|---|---|
| 1 | Canada75 | 0.0346 | 0.0047 | 65-75 | 0.034600 | 0.000000 |
| 2 | Canada85 | 0.0240 | 0.0000 | 75-85 | 0.024000 | 0.000000 |
| 3 | Congo75 | 0.0464 | 0.3385 | 65-75 | 0.046400 | 0.000000 |
| 4 | Cyprus85 | 0.0709 | 0.6000 | 75-85 | 0.070900 | 0.000000 |
| 5 | Finland75 | 0.0391 | 0.0000 | 65-75 | 0.039100 | 0.000000 |
| 6 | Germany_West85 | 0.0214 | 0.0000 | 75-85 | 0.021400 | 0.000000 |
| 7 | Ghana85 | -0.0150 | 0.0500 | 75-85 | -0.015000 | 0.000000 |
| 8 | United_States75 | 0.0155 | 0.0015 | 65-75 | 0.015500 | 0.000000 |
| 9 | Yemen85 | 0.0305 | 0.0730 | 75-85 | 0.030500 | 0.000000 |
| 10 | Denmark85 | 0.0234 | 0.0000 | 75-85 | 0.023010 | 0.000390 |
| 11 | Japan75 | 0.0636 | 0.0005 | 65-75 | 0.062519 | 0.001081 |
| 12 | Jordan85 | 0.0593 | 0.5000 | 75-85 | 0.058201 | 0.001099 |
| 13 | Sudan85 | 0.0007 | 0.7000 | 75-85 | -0.000919 | 0.001619 |
| 14 | Iran75 | 0.0538 | 0.0072 | 65-75 | 0.051880 | 0.001920 |
| 15 | Spain75 | 0.0457 | 0.0014 | 65-75 | 0.043241 | 0.002459 |
| 16 | Egypt85 | 0.0427 | 0.5500 | 75-85 | 0.038409 | 0.004291 |
| 17 | Hong_Kong85 | 0.0649 | 0.0000 | 75-85 | 0.059040 | 0.005860 |
| 18 | Bangladesh85 | 0.0133 | 0.6507 | 75-85 | 0.006816 | 0.006484 |
| 19 | Rwanda75 | 0.0590 | 0.0500 | 65-75 | 0.050266 | 0.008734 |
| 20 | Brazil75 | 0.0637 | 0.0011 | 65-75 | 0.050749 | 0.012951 |
| 21 | Syria75 | 0.0601 | 0.2500 | 65-75 | 0.046072 | 0.014028 |
| 22 | Botswana85 | 0.0512 | 0.0000 | 75-85 | 0.030626 | 0.020574 |