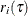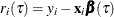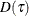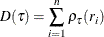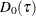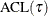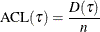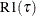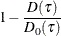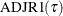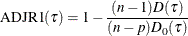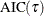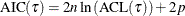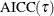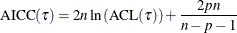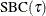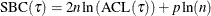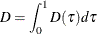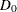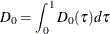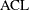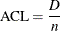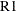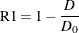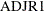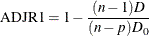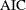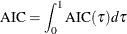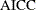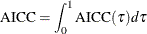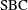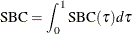The QUANTSELECT Procedure

Criteria Used in Model Selection Methods

Subsections:

PROC QUANTSELECT supports a variety of fit statistics that you can specify as criteria for the CHOOSE= , SELECT= , and STOP= method-options in the MODEL statement.

Single Quantile Effect Selection

The following fit statistics are available for single quantile effect selection:

AIC

applies the Akaike’s information criterion (Akaike 1981; Darlington 1968; Judge et al. 1985).

AICC

applies the corrected Akaike’s information criterion (Hurvich and Tsai 1989).

SBC

applies the Schwarz Bayesian information criterion (Schwarz 1978; Judge et al. 1985).

SL<(LR1 | LR2)>

specifies the significance level of a statistic used to assess an effect’s contribution to the fit when it is added to or removed from a model. LR1 specifies likelihood ratio Type I, and LR2 specifies the likelihood ratio Type II. By default, the LR1 statistic is applied.

ADJR1

applies the adjusted quantile regression R statistic.

VALIDATE

applies the average check loss for the validation data.

Table 96.11 provides formulas and definitions for these fit statistics.

Table 96.11: Formulas and Definitions for Model Fit Summary Statistics for Single Quantile Effect Selection

Statistic

Definition or Formula

n

Number of observations

p

Number of parameters including the intercept

$r_ i(\tau )$

Residual for the ith observation; $\displaystyle r_{i}(\tau ) = y_ i-\mb{x}_ i\bbeta (\tau )$

$D(\tau )$

Total sum of check losses; $\displaystyle D(\tau )= \sum _{i=1}^ n \rho _\tau (r_{i})$

$D_0(\tau )$

Total sum of check losses for intercept-only model if intercept is a forced-in effect, otherwise for empty-model.

$\mbox{ACL}(\tau )$

Average check loss; $\displaystyle \mbox{ACL}(\tau ) ={D(\tau )\over n}$

$\mbox{R1}(\tau )$

Counterpart of linear regression R-square for quantile regression; $\displaystyle 1- {D(\tau )\over D_0(\tau )}$

$\mbox{ADJR1}(\tau )$

Adjusted R1; $\displaystyle \mbox{ADJR1}(\tau )=1-{(n-1)D(\tau )\over (n-p)D_0(\tau )}$

$\mbox{AIC}(\tau )$

Akaike’s information criterion; $\displaystyle \mbox{AIC}(\tau )=2n\ln \left(\mbox{ACL}(\tau )\right)+2p$

$\mbox{AICC}(\tau )$

Corrected Akaike’s information criterion; $\displaystyle \mbox{AICC}(\tau )=2n\ln \left( \mbox{ACL}(\tau ) \right) + {2pn\over n-p-1}$

$\mbox{SBC}(\tau )$

Schwarz Bayesian information criterion; $\displaystyle \mbox{SBC}(\tau )=2n\ln \left( \mbox{ACL}(\tau ) \right) + p \ln (n) $


Quantile Process Effect Selection

The following statistics are available for quantile process effect selection:

AIC

specifies Akaike’s information criterion (Akaike 1981; Darlington 1968; Judge et al. 1985).

AICC

specifies the corrected Akaike’s information criterion (Hurvich and Tsai 1989).

SBC

specifies Schwarz Bayesian information criterion (Schwarz 1978; Judge et al. 1985).

ADJR1

specifies the adjusted quantile regression R statistic.

VALIDATE

specifies average check loss for the validation data.

Table 96.12 provides formulas and definitions for the fit statistics.

Table 96.12: Formulas and Definitions for Model Fit Summary Statistics for Quantile Process Effect Selection

Statistic

Definition or Formula

D

Integral of total sum of check losses; $\displaystyle D=\int _0^1D(\tau ) d\tau $

$D_0$

Integral of total sum of check losses for intercept-only model or empty-model if the NOINT option is used; $\displaystyle D_0=\int _0^1D_0(\tau ) d\tau $

$\mbox{ACL}$

Integral of average check loss; $\displaystyle \mbox{ACL}={D\over n}$

$\mbox{R1}$

Counterpart of linear regression R-square for quantile process regression; $\displaystyle \mbox{R1}=1- {D\over D_0}$

$\mbox{ADJR1}$

Adjusted R1; $\displaystyle \mbox{ADJR1}=1-{(n-1)D\over (n-p)D_0}$

$\mbox{AIC} $

Akaike’s information criterion; $\displaystyle \mbox{AIC}=\int _0^1\mbox{AIC}(\tau ) d\tau $

$\mbox{AICC} $

Corrected Akaike’s information criterion; $\displaystyle \mbox{AICC}=\int _0^1\mbox{AICC}(\tau ) d\tau $

$\mbox{SBC}$

Schwarz Bayesian information criterion; $\displaystyle \mbox{SBC}=\int _0^1\mbox{SBC}(\tau ) d\tau $