The QUANTSELECT Procedure

Displayed Output

Subsections:

The following sections describe the output that is displayed by PROC QUANTSELECT. The output is organized into various tables, which are discussed in the order of appearance. The contents of a table might change depending on the options you specify.

Model Information

The "Model Information" table displays basic information about the data sets and the settings used to control effect selection. These settings include the following:

  • the selection method

  • the criteria used to select effects, stop the selection, and choose the selected model

  • the effect hierarchy enforced

The ODS name of the "Model Information" table is ModelInfo.

Number of Observations

The "Number of Observations" table displays the number of observations read from the input data set and the number of observations used in the analysis. If you use a PARTITION statement, the table also displays the number of observations used for each data role. If you specify TESTDATA= or VALDATA= data sets in the PROC QUANTSELECT statement, then "Number of Observations" tables are also produced for these data sets. The ODS name of the "Number of Observations" table is NObs.

Class Level Information

The "Class Level Information" table lists the levels of every variable specified in the CLASS statement. The ODS name of the "Class Level Information" table is ClassLevelInfo.

Class Level Coding

The "Class Level Coding" table shows the coding used for every variable specified in the CLASS statement. The ODS name of the "Class Level Coding" table is ClassLevelCoding.

Dimensions

The "Dimensions" table displays information about the number of effects and the number of parameters from which the selected model is chosen. If you use split classification variables, then this table also includes the number of effects after splitting is taken into account. The ODS name of the "Dimensions" table is Dimensions.

Candidates

The "Candidates" table displays the effect name and value of the criterion used to select entering or departing effects at each step of the selection process. The effects are displayed in sorted order from best to worst of the selection criterion. You request this table with the DETAILS= option in the MODEL statement. The ODS name of the "Candidates" table is either EntryCandidates for addition candidates or RemovalCandidates for removal candidates.

Selection Summary

The "Selection Summary" table displays details about the sequence of steps of the selection process. For each step, the effect that entered or dropped out is displayed along with the statistics used to select the effect, stop the selection, and choose the selected model. You can request that additional statistics be displayed with the STATS= option in the MODEL statement. For all criteria that you can use for effect selection, the steps at which the optimal values of these criteria occur are also indicated. The ODS name of the "Selection Summary" table is SelectionSummary.

Stop Reason

The "Stop Reason" table displays the reason why the selection stopped. Table 96.14 shows the possible stop reasons.

Table 96.14: Reasons for Stopping

Stop Reason

Description

1

The selected model is a perfect fit.

2

The specified maximum number of steps has been reached.

3

The specified maximum number of effects are in the model.

4

The specified minimum number of effects are in the model.

5

The stopping criterion found a local optimum.

6

No suitable add or drop candidate is available.

7

All effects are in the model.

8

All effects have been dropped.

9

The sequence of effect additions and removals is cycling.

10

Adding or dropping any effect does not improve the SELECT= criterion.

11

No effect is significant at the specified significance level for entry or significance level for staying levels.

12

All remaining effects are required.


The ODS name of the "Stop Reason" table is StopReason.

Selection Reason

The "Selection Reason" table displays how the final selected model is determined. Table 96.15 shows the possible selection reasons:

Table 96.15: Selection Reasons

Selection Reason

Description

1

The last valid model that occurs in the selection process is the final model.

2

The first model with the minimum CHOOSE= criterion value in the selection process is the final model.


The ODS name of the "Selection Reason" table is SelectionReason.

Selected Effects

The "Selected Effects" table displays a string that contains the list of effects in the selected model. The ODS name of the "Selected Effects" table is SelectedEffects.

Fit Statistics

The "Fit Statistics" table displays fit statistics for the selected model. The statistics displayed include the following:

  • OBJ, the sum of check losses. It is calculated as the minimized objective function value for the fit.

  • R1, a measure between 0 and 1 that indicates the portion of the (corrected) total variation attributed to the fit rather than left to residual error. It is calculated as one minus OBJ(Model) divided by OBJ(Total).

  • Adj R1, the adjusted 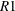$R1$, a version of 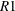$R1$ that has been adjusted for degrees of freedom. It is calculated as

    \[ \bar{R1} = 1 - \frac{(n-i)(1-R1)}{n-p} \]

    where i is equal to 1 if there is an intercept and 0 otherwise, n is the number of observations used to fit the model, and p is the number of parameters in the model.

  • fit criteria AIC, AICC, and SBC.

  • the average check losses (ACL) on the training, validation, and test data. See the section Using Validation and Test Data for details.

You can request "Fit Statistics" tables for the models at each step of the selection process with the DETAILS= option in the MODEL statement. The ODS name of the "Fit Statistics" table is FitStatistics.

Parameter Estimates

The "Parameter Estimates" table displays the parameters in the selected model and their estimates. The following information is displayed for each parameter in the selected model:

  • the parameter label that includes the effect name and level information for effects that contain classification variables

  • the degrees of freedom (DF) for the parameter. There is one degree of freedom unless the model is not full rank.

  • the parameter estimate

  • the standard parameter estimate, which is computed on a standardized design matrix. Let 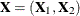$\bX =(\bX _1,\bX _2)$ denote the original design matrix, where 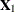$\bX _1$ is the submatrix for all the forced-in effects, and 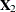$\bX _2$ is the submatrix for the rest of the effects that are subject to selection. Let

    \[ \bX ^*_2=\left[\bI -\bX _1({\bX _1}’\bX _1)^{-1}{\bX _1}’\right]\bX _2 \mbox{ and } \bX ^{**}_2= s_ Y\bX ^*_2 \left[{\mbox{diag}({\bX ^*_2}’\bX ^*_2) \over {n - p_1}}\right]^{-{1\over 2}} \]

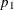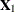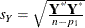    where $p_1$ is the rank of $\bX _1$ and $ s_ Y = \sqrt {\frac{\bY ^{*\prime }\bY ^*}{n - p_{1}}}$ with $\bY ^* = \left[\bI -\bX _1({\bX _1}’\bX _1)^{-1}{\bX _1}’\right]\bY $.

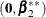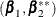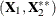    Then standard parameter estimates are defined as $(\mb{0},\bbeta ^{**}_2)$, where $(\bbeta _1, \bbeta ^{**}_2)$ are the parameter estimates computed on the standardized design matrix $(\bX _1,\bX ^{**}_2)$.

You can also use the DETAILS= option in the MODEL statement to request "Parameter Estimates" tables for the models at each step of the selection process. The ODS name of the "Parameter Estimates" table is ParameterEstimates.

Parameter Estimates for Quantile Process

The "Parameter Estimates for Quantile Process" table contains the parameter estimates for the quantile process of the final selected model. The following statements show how you can request the output data set of this table by using the ODS OUTPUT statement: 

proc quantselect data=Data;
   ods output ProcessEst=outProcessEst;
   model y=x1-x10 / selection=forward quantile=process;
run;
proc print data=outProcessEst;
run;

The output data set contains the following variables:

  • QuantileLabel, the label of quantile levels

  • QuantileLevel, the quantile levels

  • variables for parameter estimates

Given the quantile-level grid for the quantile process,

\[ \left\{ 0=\tau _{(0)}\le \tau _{(1)}\le \cdots \le \tau _{(s)}\le \tau _{(s+1)}=1\right\} \]

The ith observation in the "Parameter Estimates for Quantile Process" table corresponds to the optimal solution of the ith quantile level in the quantile-level grid. The ith QuantileLabel value is in the form of ti, and the ith QuantileLevel value is equal to 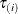$\tau _{(i)}$. For more information about the quantile-level grid, see the section Quantile Process Regression.