The QUANTSELECT Procedure

Quasi-Likelihood Ratio Tests

Under the iid assumption, Koenker and Machado (1999) proposed two types of quasi-likelihood ratio tests for quantile regression, where the error distribution is flexible but not limited to the asymmetric Laplace distribution. The Type I test score, LR1, is defined as

\[ {2(D_1(\tau )-D_2(\tau ))\over \tau (1-\tau )\hat{s}} \]

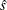where $\hat{s}$ is the estimated sparsity function, 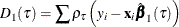$\displaystyle D_1(\tau )=\sum \rho _\tau \left(y_ i-\mb{x}_ i\hat{\bbeta }_1(\tau )\right)$ is the sum of check losses for the reduced model, and 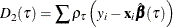$\displaystyle D_2(\tau )=\sum \rho _\tau \left(y_ i-\mb{x}_ i\hat{\bbeta }(\tau )\right)$ is the sum of check losses for the extended model. The Type II test score, LR2, is defined as

\[ {2D_2(\tau )\left(\log (D_1(\tau ))-\log (D_2(\tau ))\right)\over \tau (1-\tau )\hat{s}} \]

Under the null hypothesis that the reduced model is the true model, both LR1 and LR2 follow a $\chi ^2$ distribution with $df=df_2-df_1$ degrees of freedom, where $df_1$ and $df_2$ are the degrees of freedom for the reduced model and the extended model, respectively.

If you specify the TEST=LR1 option in the MODEL statement, the QUANTSELECT procedure uses LR1 score to compute the significance level. Or you can use the substitutable TEST=LR2 option for computing the significance level on Type II quasi-likelihood ratio test.

Under the iid assumption, the sparsity function is defined as $s(\tau )=1/f(F^{-1}(\tau ))$. Here the distribution of errors F is flexible but not limited to the asymmetric Laplace distribution. The algorithm for estimating $s(\tau )$ is as follows:

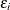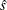  1. Fit a quantile regression model and compute the residuals. Each residual $r_ i=y_ i-\mb{x}_ i’\hat{\bbeta }(\tau )$ can be viewed as an estimated realization of the corresponding error $\epsilon _ i$. Then $\hat{s}$ is computed on the reduced model for testing the entry effect and on the extended model for testing the removal effect.

  2. Compute quantile-level bandwidth $h_ n$. The QUANTSELECT procedure computes the Bofinger bandwidth, which is an optimizer of mean squared error for standard density estimation:

    \[ h_ n = n^{-1\slash 5} ( {4.5v^2(\tau )} )^{1\slash 5} \]

    The quantity

    \[ v(\tau ) = {\frac{s(\tau )}{s^{(2)}(\tau )}} = {\frac{f^2}{2(f^{(1)} \slash f)^2 + [(f^{(1)} \slash f)^2 - f^{(2)}\slash f ] }} \]

    is not sensitive to f and can be estimated by assuming f is Gaussian as

    \[ \hat{v}(\tau )={{\exp (-q^2)} \over 2\pi (q^2+1)} \mbox{ with } q=\Phi ^{-1}(\tau ) \]

  3. Compute residual quantiles $\hat{F}^{-1}(\tau _0)$ and $\hat{F}^{-1}(\tau _1)$ as follows:

    1. Set $\tau _0=\max (0,\tau -h_ n)$ and $\tau _1=\min (1,\tau +h_ n)$.

    2. Use the equation

      \[ {\hat F}^{-1}(t) = \left\{ \begin{array}{ll} r_{(1)} & {\mbox{if }} t\in [0, 1\slash 2n) \\ \lambda r_{(i+1)} + (1-\lambda ) r_{(i)} & {\mbox{if }} t\in [(i-0.5)\slash n, (i+0.5)\slash n) \\ r_{(n)} & {\mbox{if }} t\in [(2n-1), 1] \\ \end{array} \right. \]

      where $r_{(i)}$ is the ith smallest residual and $\lambda =t-(i-0.5)\slash n$.

    3. If ${\hat F}^{-1}(\tau _0)={\hat F}^{-1}(\tau _1)$, find i that satisfies $r_{(i)}<{\hat F}^{-1}(\tau _0)$ and $r_{(i+1)}\ge {\hat F}^{-1}(\tau _0)$. If such an i exists, reset $\tau _0=(i-0.5)/n$ so that ${\hat F}^{-1}(\tau _0)=r_{(i)}$. Also find j that satisfies $r_{(j)}>{\hat F}^{-1}(\tau _1)$ and $r_{(j-1)}\le {\hat F}^{-1}(\tau _1)$. If such a j exists, reset $\tau _1=(j-0.5)/n$ so that ${\hat F}^{-1}(\tau _1)=r_{(j)}$.

  4. Estimate the sparsity function $s(\tau )$ as

    \[ \hat{s}(\tau )={{\hat{F}^{-1}(\tau _1)-\hat{F}^{-1}(\tau _0)} \over {\tau _1-\tau _0}} \]

Because a real data set might not follow the null hypothesis and the iid assumptions, the LR1 and LR2 scores that are used for quantile regression effect selection often do not follow a $\chi ^2$ distribution. Hence, the SLENTRY and SLSTAY values cannot reliably be viewed as probabilities. One way to address this difficulty is to treat the SLENTRY and SLSTAY values only as criteria for comparing importance levels of effect candidates at each selection step, and not to explain these values as probabilities.