The QUANTSELECT Procedure
Quasi-Likelihood Information Criteria
Given quantile level 
, assume that the distribution of 
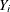conditional on 
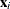follows the linear model
![\[ Y_ i = \mb{x}_ i^{\prime }\bbeta + \epsilon _ i \]](images/statug_qrsel0031.png)
where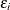 
for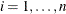 
are iid in distribution F. Further assume that F is an asymmetric Laplace distribution whose density function is
![\[ f_\tau (r)={\tau (1-\tau )\over \sigma }\exp \left(-{\rho _\tau (r)\over \sigma }\right) \]](images/statug_qrsel0034.png)
where 
is the scale parameter. Then, the associated -log likelihood function is
![\[ l_\tau (\bbeta ,\sigma )=n\log (\sigma )+ \sigma ^{-1}\sum _{i=1}^ n\rho _\tau (y_ i-\mb{x}_ i’\bbeta )-n\log (\tau (1-\tau )) \]](images/statug_qrsel0036.png)
Under these settings, the maximum likelihood estimate (MLE) of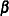 
is the same as the relevant level quantile regression solution
![\[ \hat{\bbeta }(\tau )=\underset {\bbeta }{\mr{arg min}}\sum _{i=1}^ n \rho _\tau \left(y_ i-\mb{x}_ i^{\prime }\bbeta \right) \]](images/statug_qrsel0037.png)
The MLE for is
![\[ \hat{\sigma }(\tau )=n^{-1}\sum _{i=1}^ n \rho _\tau \left(y_ i-\mb{x}_ i^{\prime }\hat{\bbeta }(\tau )\right) \]](images/statug_qrsel0038.png)
where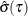 
equals the level average check loss,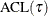 
, for the quantile regression solution.
According to the general form of Akaike’s information criterion,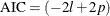 
, the quasi-likelihood AIC for quantile regression is
![\[ \mbox{AIC}(\tau )=2n\ln \left( \mbox{ACL}(\tau ) \right) + 2p \]](images/statug_qrsel0042.png)
where p is the degrees of freedom for the fitted model.
Similarly, the quasi-likelihood corrected AIC and Schwarz Bayesian information criterion can be formulated respectively as follows:
![\[ \mbox{AICC}(\tau )=2n\ln \left(\mbox{ACL}(\tau )\right)+{2pn\over n-p-1} \]](images/statug_qrsel0043.png)
![\[ \mbox{SBC}(\tau )=2n\ln \left(\mbox{ACL}(\tau )\right)+p\ln (n) \]](images/statug_qrsel0044.png)
In fact, the quasi-likelihood AIC, AICC, and SBC are fairly robust, and they can be used to select effects for data sets without the iid assumption in asymmetric Laplace distribution. See Simulation Study for a simulation study that applies SBC for effect selection on a data set that is generated from a naive instrumental model (Chernozhukov and Hansen 2008).