The QUANTSELECT Procedure
Observation Quantile Level
The observation quantile level of a valid observation, 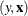 , is defined as
, is defined as 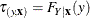 , where
, where 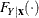 denotes the cumulative distribution function (CDF) for the y’s underlying distribution conditional on
denotes the cumulative distribution function (CDF) for the y’s underlying distribution conditional on  . For the CDF that is continuous at y, the equation
. For the CDF that is continuous at y, the equation 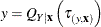 holds because the quantile function is inversely related to the CDF. Ideally, if
holds because the quantile function is inversely related to the CDF. Ideally, if 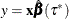 for a unique
for a unique ![$\tau ^*\in [0,1]$](images/statug_qrsel0097.png) and some quantile-regression optimal solution
and some quantile-regression optimal solution 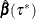 , then
, then 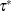 is a reasonable estimation for
is a reasonable estimation for 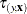 , written as
, written as 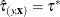 . However, such a
. However, such a 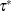 might not exist or is nonunique in practice. The following steps show how the QUANTSELECT procedure estimates the observation
quantile level
might not exist or is nonunique in practice. The following steps show how the QUANTSELECT procedure estimates the observation
quantile level 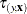 via quantile process regression:
via quantile process regression:
-
Fit the quantile process regression model and label its quantile-level grid as follows:
![\[ \left\{ 0=\tau _{(0)}\le \tau _{(1)}\le \cdots \le \tau _{(s)}\le \tau _{(s+1)}=1\right\} \]](images/statug_qrsel0101.png)
-
Compute quantile predictions conditional on
 in the quantile-level grid:
in the quantile-level grid: 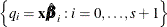 .
.
-
Sort
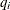 ’s to avoid crossing, such that
’s to avoid crossing, such that 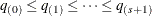 .
.
-
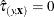 if
if 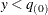 , or
, or 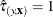 if
if 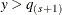 .
.
-
Otherwise, search index j such that
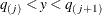 . If such a j exists,
. If such a j exists,
![\[ \hat{\tau }_{(y,\mb{x})} = \left({y-q_{(j)} \over q_{(j+1)}-q_{(j)}}\right)\tau _{(j+1)} +\left({q_{(j+1)}-y \over q_{(j+1)}-q_{(j)}}\right)\tau _{(j)} \]](images/statug_qrsel0110.png)
-
Otherwise, search j and k such that
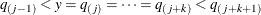 , and set
, and set 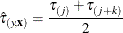 . Here, define
. Here, define 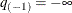 and
and 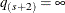 .
.
