The QUANTSELECT Procedure
Quantile Regression for Extremal Quantile Levels
A quantile level  is extremal if
is extremal if  is equal to or approaching 0 or 1. The solution for an extremal quantile-level quantile regression problem can be nonunique
because the parameter estimate of the intercept effect can be arbitrarily small or large. In a quantile process regression
toward the direction of the specified extremal quantile level, the tightest solution refers to the first solution whose quantile-level
range includes the specified extremal quantile level. Among all the valid solutions for an extremal quantile-level quantile
regression problem, the tightest solution can generalize the terminology of sample minimum and sample maximum.
is equal to or approaching 0 or 1. The solution for an extremal quantile-level quantile regression problem can be nonunique
because the parameter estimate of the intercept effect can be arbitrarily small or large. In a quantile process regression
toward the direction of the specified extremal quantile level, the tightest solution refers to the first solution whose quantile-level
range includes the specified extremal quantile level. Among all the valid solutions for an extremal quantile-level quantile
regression problem, the tightest solution can generalize the terminology of sample minimum and sample maximum.
The QUANTSELECT procedure computes the tightest solution for an extremal quantile-level quantile regression problem by using
the ALGORITHM=SIMPLEX algorithm. If ![$\displaystyle \tau \in \left[{1\over 4n},1-{1\over 4n}\right]$](images/statug_qrsel0115.png) ,
,  is not extremal. Otherwise, follow these steps:
is not extremal. Otherwise, follow these steps:
-
Set
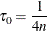
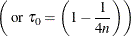 .
.
-
Compute
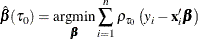 .
.
-
Find the quantile-level lower limit (or upper limit),
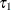 , such that
, such that 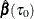 is still optimal at
is still optimal at 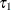 .
.
-
If
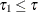 (or
(or 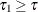 ), return
), return 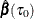 . Otherwise, update
. Otherwise, update 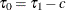 (or
(or 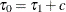 ) for a small tolerance
) for a small tolerance 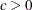 , and go to step 2.
, and go to step 2.
