The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
ESTIMATE Statement
-
ESTIMATE <'label'> estimate-specification <(divisor=n)><, …<'label'> estimate-specification <(divisor=n)>></ options>;
The ESTIMATE statement provides a mechanism for obtaining custom hypothesis tests. Estimates are formed as linear estimable
functions of the form 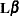 . You can perform hypothesis tests for the estimable functions, construct confidence limits, and obtain specific nonlinear
transformations.
. You can perform hypothesis tests for the estimable functions, construct confidence limits, and obtain specific nonlinear
transformations.
Table 72.5 summarizes the options available in the ESTIMATE statement.
Table 72.5: ESTIMATE Statement Options
|
Option |
Description |
|---|---|
|
Construction and Computation of Estimable Functions |
|
|
Specifies a list of values to divide the coefficients |
|
|
Suppresses the automatic fill-in of coefficients for higher-order effects |
|
|
Tunes the estimability checking difference |
|
|
Degrees of Freedom and p-values |
|
|
Determines the method for multiple comparison adjustment of estimates |
|
|
Determines the confidence level ( |
|
|
Performs one-sided, lower-tailed inference |
|
|
Adjusts multiplicity-corrected p-values further in a step-down fashion |
|
|
Specifies values under the null hypothesis for tests |
|
|
Performs one-sided, upper-tailed inference |
|
|
Statistical Output |
|
|
Constructs confidence limits |
|
|
Displays the correlation matrix of estimates |
|
|
Displays the covariance matrix of estimates |
|
|
Prints the |
|
|
Produces a joint F or chi-square test for the estimable functions |
|
|
Requests ODS statistical graphics if the analysis is sampling-based |
|
|
Specifies the seed for computations that depend on random numbers |
|
|
Generalized Linear Modeling |
|
|
Specifies how to construct estimable functions with multinomial data |
|
|
Exponentiates and displays estimates |
|
|
Computes and displays estimates and standard errors on the inverse linked scale |
|
For details about the syntax of the ESTIMATE statement, see the section ESTIMATE Statement in Chapter 19: Shared Concepts and Topics.